
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,对任意的
上的奇函数,对任意的![]() ,均有
,均有![]() .当
.当![]() 时,
时,![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线C1:ρsin2θ=4cosθ.以极点为坐标原点,极轴为x轴正半轴建立直角坐标系xOy,曲线C2的参数方程为: ![]() ,(θ∈[﹣
,(θ∈[﹣ ![]() ,
, ![]() ]),曲线C:
]),曲线C: 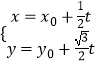 (t为参数).
(t为参数).
(Ⅰ)求C1的直角坐标方程;
(Ⅱ)C与C1相交于A,B,与C2相切于点Q,求|AQ|﹣|BQ|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,直线PA⊥平面ABCD,AD∥BC,AB⊥AD,BC=2AB=2AD=4BE=4.
(I)求证:直线DE⊥平面PAC.
(Ⅱ)若直线PE与平面PAC所成的角的正弦值为 ![]() ,求二面角A﹣PC﹣D的平面角的余弦值.
,求二面角A﹣PC﹣D的平面角的余弦值.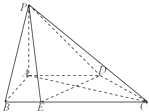
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)满足f(x+1)=﹣f(x),且f(x)是偶函数,当x∈[0,1]时,f(x)=x2 , 若在区间[﹣1,3]内,函数g(x)=f(x)﹣kx﹣k有4个零点,则实数k的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=sin(x+ ![]() )图象上各点的横坐标缩短到原来的
)图象上各点的横坐标缩短到原来的 ![]() 倍(纵坐标不变),再把得到的图象向右平移
倍(纵坐标不变),再把得到的图象向右平移 ![]() 个单位,得到的新图象的函数解析式为g(x)= , g(x)的单调递减区间是 .
个单位,得到的新图象的函数解析式为g(x)= , g(x)的单调递减区间是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两超市同时开业,第一年的全年销售额为a万元,由于经营方式不同,甲超市前n年的总销售额为![]() (n2-n+2)万元,乙超市第n年的销售额比前一年销售额多a
(n2-n+2)万元,乙超市第n年的销售额比前一年销售额多a![]() 万元.
万元.
(1)求甲、乙两超市第n年销售额的表达式;
(2)若其中某一超市的年销售额不足另一超市的年销售额的50%,则该超市将被另一超市收购,判断哪一超市有可能被收购?如果有这种情况,将会出现在第几年?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊人常用小石子在沙滩上摆成各种形状来研究数,例如:

他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16,…这样的数为正方形数.下列数中既是三角形数又是正方形数的是
A. 289 B. 1 024 C. 1 225 D. 1 378
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com