
【题目】已知函数![]() ,
,![]() .
.
(1)是否存在![]() 及过原点的直线
及过原点的直线![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() ,
,![]() 均相切?若存在,求
均相切?若存在,求![]() 的值及直线
的值及直线![]() 的方程;若不存在,请说明理由;
的方程;若不存在,请说明理由;
(2)若函数![]() 在区间
在区间![]() 上是单调函数,求
上是单调函数,求![]() 的取值范围.
的取值范围.
【答案】(1)存在![]() 及
及![]() :
:![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() ,
,![]() 均相切;(2)
均相切;(2)![]() 的取值范围是
的取值范围是![]() .
.
【解析】
试题分析:对问题(1),根据导数的几何意义以及过原点的直线![]() 是曲线
是曲线![]() ,
,![]() 的公切线,从而可求出直线
的公切线,从而可求出直线![]() 的方程以及
的方程以及![]() 的值;对于问题(2),通过对函数
的值;对于问题(2),通过对函数![]() 进行求导并结合对实数
进行求导并结合对实数![]() 的分类讨论即可求出
的分类讨论即可求出![]() 的取值范围.
的取值范围.
试题解析:(1)∵![]() ,设曲线
,设曲线![]() 在点
在点![]() 处切线过原点,则切线方程为
处切线过原点,则切线方程为![]() ,
,
∵点![]() 在切线上,∴
在切线上,∴![]() ,∴
,∴![]() ,∴切线方程为
,∴切线方程为![]() ,设直线
,设直线![]() 与曲线
与曲线![]() 切于点
切于点![]() ,∵
,∵![]() ,∴
,∴![]() ,
,![]() .
.
又∵![]() ,∴
,∴![]() ,∴
,∴![]() ,解得
,解得![]() ,
,
∴![]() .故存在
.故存在![]() 及
及![]() :
:![]() ,使得直线
,使得直线![]() 与曲线
与曲线![]() ,
,![]() 均相切.
均相切.
(2)![]() ,
,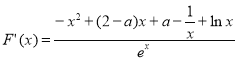 ,
,
令![]() ,则
,则![]() ,易知
,易知![]() 在
在![]() 上单调递减,从而
上单调递减,从而![]() .
.
①当![]() 时,即
时,即![]() 时,
时,![]() ,
,![]() 在区间
在区间![]() 上单调递增,∵
上单调递增,∵![]() ,∴
,∴![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立.
上恒成立.
∴![]() 在区间
在区间![]() 上单调递减,∴
上单调递减,∴![]() 满足题意.
满足题意.
②当![]() 时,即
时,即![]() 时,
时,![]() ,当
,当![]() 且
且![]() 时,
时,![]() ,故函数
,故函数![]() 存在唯一零点
存在唯一零点![]() ,且
,且![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,又∵
上单调递减,又∵![]() ,∴
,∴![]() 在
在![]() 上单调递增.
上单调递增.
注意到![]() ,∴
,∴![]() 在
在![]() 上单调递减,这与
上单调递减,这与![]() 在区间
在区间![]() 上是单调函数矛盾,∴
上是单调函数矛盾,∴![]() 不合题意.
不合题意.
综合①②得,![]() 的取值范围是
的取值范围是![]() .
.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源: 题型:
【题目】下面图①、图②是某校调查部分学生是否知道父母亲生日情况的扇形和条形统计图:
根据上图信息,解答下列问题:
(1)求本次被调查学生的人数,并补全条形统计图;
(2)若全校共有2700名学生,你估计这所学校有多少名学生知道父母亲的生日?
(3)通过对以上数据的分析,你有何感想?(用一句话回答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C上任一点P到点F(1,0)的距离比它到直线![]() 的距离少1.
的距离少1.
(1)求曲线C的方程;
(2)过点![]() 作两条倾斜角互补的直线与曲线C分别交于点A、B,试问:直线AB的斜率是否为定值,请说明理由.
作两条倾斜角互补的直线与曲线C分别交于点A、B,试问:直线AB的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)若函数![]() 有且只有一个极值点,求实数
有且只有一个极值点,求实数![]() 的取值范围;
的取值范围;
(2)对于函数![]() ,
,![]() ,
,![]() ,若对于区间
,若对于区间![]() 上的任意一个
上的任意一个![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 是函数
是函数![]() ,
,![]() 在区间
在区间![]() 上的一个“分界函数”.已知
上的一个“分界函数”.已知![]() ,
,![]() ,问是否存在实数
,问是否存在实数![]() ,使得函数
,使得函数![]() 是函数
是函数![]() ,
,![]() 在区间
在区间![]() 上的一个“分界函数”?若存在,求实数
上的一个“分界函数”?若存在,求实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com