
【题目】过点![]() 的直线
的直线![]() 被曲线
被曲线![]() 截得的弦长为2,则直线
截得的弦长为2,则直线![]() 的方程为______.
的方程为______.
【答案】x=3或5x+12y﹣3=0.
【解析】
曲线化简得:(x﹣1)2+(y﹣2)2=5,根据圆的弦长公式2![]() ,d=2,分直线l的斜率不存在与存在两种情况,利用点到直线距离公式计算即可得到结果.
,d=2,分直线l的斜率不存在与存在两种情况,利用点到直线距离公式计算即可得到结果.
曲线的方程化简得:(x﹣1)2+(y﹣2)2=5,表示圆心为(1,2),半径为![]() 的圆,
的圆,
由圆的弦长公式2![]() ,可得圆心到直线l的距离d=2,
,可得圆心到直线l的距离d=2,
当直线l的斜率不存在时,直线l的方程为:x=3.此时圆心到x=3的距离为2,满足题意;
当直线l的斜率存在时,设直线l的方程为:y=k(x﹣3)﹣1.即kx﹣y﹣3k﹣1=0.
由![]() k
k![]() ,直线l的方程为:5x+12y﹣3=0.
,直线l的方程为:5x+12y﹣3=0.
故答案为x=3或5x+12y﹣3=0.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的长轴长为6,离心率为
的长轴长为6,离心率为![]() .
.
(1)求椭圆C的标准方程;
(2)设椭圆C的左右焦点分别为![]() ,
,![]() ,左右顶点分别为A,B,点M,N为椭圆C上位于x轴上方的两点,且
,左右顶点分别为A,B,点M,N为椭圆C上位于x轴上方的两点,且![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,记直线AM,BN的斜率分别为
,记直线AM,BN的斜率分别为![]() ,试证明:
,试证明:![]() 的值为定值.
的值为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的焦距为
的焦距为![]() ,且C过点
,且C过点![]() .
.
(1)求椭圆C的方程;
(2)设![]() 、
、![]() 分别是椭圆C的下顶点和上顶点,P是椭圆上异于
分别是椭圆C的下顶点和上顶点,P是椭圆上异于![]() 、
、![]() 的任意一点,过点P作
的任意一点,过点P作![]() 轴于M,N为线段PM的中点,直线
轴于M,N为线段PM的中点,直线![]() 与直线
与直线![]() 交于点D,E为线段
交于点D,E为线段![]() 的中点,O为坐标原点,则
的中点,O为坐标原点,则![]() 是否为定值,若是,请求出定值;若不是,请说明理由.
是否为定值,若是,请求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的定义域为
的定义域为![]() ,
,![]() ,使得不等式
,使得不等式![]() 成立,关于
成立,关于![]() 的不等式
的不等式![]() 的解集记为
的解集记为![]() .
.
(1)若![]() 为真,求实数
为真,求实数![]() 的取值集合
的取值集合![]() ;
;
(2)在(1)的条件下,若![]() 是
是![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“搜索指数”是网民通过搜索引擎,以每天搜索关键词的次数为基础所得到的统计指标.“搜索指数”越大,表示网民对该关键词的搜索次数越多,对该关键词相关的信息关注度也越高.下图是2017年9月到2018年2月这半年中,某个关键词的搜索指数变化的走势图.

根据该走势图,下列结论正确的是( )
A. 这半年中,网民对该关键词相关的信息关注度呈周期性变化
B. 这半年中,网民对该关键词相关的信息关注度不断减弱
C. 从网民对该关键词的搜索指数来看,去年10月份的方差小于11月份的方差
D. 从网民对该关键词的搜索指数来看,去年12月份的平均值大于今年1月份的平均值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,其左,右焦点分别为
,其左,右焦点分别为![]() ,
,![]() ,点P是坐标平面内一点,且
,点P是坐标平面内一点,且![]() ,
,![]() ,其中O为坐标原点.
,其中O为坐标原点.
(1)求椭圆C的方程;
(2)过点![]() ,且斜率为
,且斜率为![]() 的动直线l交椭圆于A,B两点,求弦AB的垂直平分线在
的动直线l交椭圆于A,B两点,求弦AB的垂直平分线在![]() 轴上截距的最大值.
轴上截距的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
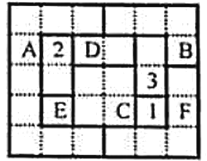
【题目】四色猜想是世界三大数学猜想之一,1976年美国数学家阿佩尔与哈肯证明了四色定理.其内容是:“任意一张平面地图只用四种颜色就能使具有共同边界的国家涂上不同的颜色.”用数学语言表示为“将平面任意地细分为不相重叠的区域,每一个区域总可以用1,2,3,4四个数字之一标记,而不会使相邻的两个区域得到相同的数字.”如图,网格纸上小正方形的边长为1,粗实线围成的各区域(如区域D由两个边长为1的小正方形构成)上分别标有数字1,2,3,4的四色地图符合四色定理,区域A、B、C、D、E、F标记的数字丢失若在该四色地图上随机取一点,则恰好取在标记为4的区域的概率是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com