设数列{an}的前n项和为Sn,关于数列{an}有下列四个命题:
①若{an}既是等差数列又是等比数列,则Sn=na1;
②若Sn=2+(-1)n,则{an}是等比数列;
③若Sn=an2+bn(a,b∈R),则{an}是等差数列;
④若Sn=pn,则无论p取何值时{an}一定不是等比数列.
其中正确命题的序号是 .
【答案】
分析:对于①,直接根据既是等差数列又是等比数列的数列特点来判断即可;
对于②④,直接利用其前n项和,求出通项公式即可判断;
对于③,直接利用等差数列前n项和公式即可的出结论.
解答:解:①若{a
n}既是等差数列又是等比数列,则数列为非0常数列,既a
n=a
1,则S
n=na
1成立;
②若S
n=2+(-1)
n,当n≥2时,a
n=S
n-S
n-1=(-1)
n-1-(-1)
n,而a
1=2+(-1)
1=1不适合上式,所以{a
n}不是等比数列,
③因为{a
n}是等差数列时,
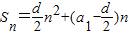
符合S
n=an
2+bn(a,b∈R)的形式,故③成立;
④若S
n=p
n,当n≥2时,a
n=S
n-S
n-1=p
n-p
n-1=p
n-1(p-1),而a
1=S
1=p不适合上式,所以{a
n}不是等比数列;
故只有①③④为真命题.
故答案为:①③④.
点评:本题主要 考查等差数列和等比数列的基础知识.若{a
n}既是等差数列又是等比数列,则数列为非0常数列,既a
n=a
1,S
n=na
1.

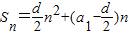 符合Sn=an2+bn(a,b∈R)的形式,故③成立;
符合Sn=an2+bn(a,b∈R)的形式,故③成立;
