Question

已知二次函数f（x）=ax²+bx+c的图象经过点（-1，3），（0，0），（2，0）．
（Ⅰ）求f（x）的解析式；
（Ⅱ）若?x∈[0，3]，3t-t²-3≤f（x）≤12-t²成立，求t的取值范围．

Answer 1

解：（Ⅰ）由题意，设f（x）=ax（x-2）
将（-1，3）代入，可得a=1
∴f（x）=x（x-2）
（Ⅱ）要使?x∈[0，3]，3t-t²-3≤f（x）≤12-t²成立，只需要3t-t²-3≤f（x）_min，且f（x）_max≤12-t²即可．
∵f（x）=x（x-2）=（x-1）²-1，x∈[0，3]，
∴x=1时，f（x）_min=-1，x=3时，f（x）_max=3
∴3t-t²-3≤-1，且3≤12-t²
∴
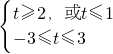
∴-3≤t≤1或2≤t≤3．
分析：（Ⅰ）将函数解析式假设成两点式，即f（x）=ax（x-2），再将（-1，3）代入，可得a=1，从而得到函数的解析式；
（Ⅱ）要使?x∈[0，3]，3t-t²-3≤f（x）≤12-t²成立，只需要3t-t²-3≤f（x）_min，且f（x）_max≤12-t²即可．将函数配方f（x）=x（x-2）=（x-1）²-1，根据x∈[0，3]，可得f（x）_min与f（x）_max，从而建立不等式可求t的取值范围
点评：本题的考点是函数恒成立问题，主要考查待定系数法求函数的解析式，考查利用最值法求解恒成立问题，解题的根据是将?x∈[0，3]，3t-t²-3≤f（x）≤12-t²成立，转化为3t-t²-3≤f（x）_min，且f（x）_max≤12-t²．