

分析 该几何体是由半个圆柱与一个三棱柱拼接而成,代入柱体体积公式,可得答案.
解答 解:该几何体是由半个圆柱(该圆柱的底面圆半径是1,高是2)与一个三棱柱(该棱柱的底面面积等于$\frac{1}{2}×2×\sqrt{3}=\sqrt{3}$,高是2)拼接而成,
其体积等于$\frac{1}{2}×π×{1}^{2}×2+\frac{1}{2}×2×\sqrt{3}×2=2\sqrt{3}+π$,
故答案为:$2\sqrt{3}+π$.
点评 本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.在2010~2014年的课标版高考试卷中,每年都要考查三视图的试题.2010年考查的是由三视图判断几何体的形状,2011年考查的是由三视图中的两个判断第三个,2012年考查的是根据三视图求几何体的体积,2013年考查的是根据三视图求几何体的体积,2014年考查的是根据三视图求多面体的最长的棱,可见每年的集合试题都是以三视图为命题背景,以几何体形状、面积、体积等为命题载体,因此本试卷命制了根据视图求几何体体积的试题作为第14题.试题设计了组合体的三视图,为考生搭建了自主探究的活动平台,使不同基础和能力的考生得以发挥.试题关注在新课程教学中学生学习方式的多样性,有利于新课程理念在教学中的落实.把几何体的三视图还原成原几何体,这不仅需要很好的空间想象能力,而且也要充分理解“长对正、高平齐、宽相等”,否则极易引起失误


 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
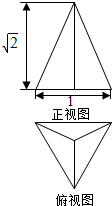 已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )
已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为( )| A. | $\frac{\sqrt{6}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{6}}{4}$ | D. | $\frac{\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{2}$+1 | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{17}{2}$ | B. | $\frac{20}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{25}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com