
【题目】设函数f (x)=ln x-x+1.
(1)讨论函数f (x)的单调性;
(2)证明当x∈(1,+∞)时, ![]() ;
;
(3)设c>1,证明当x∈(0,1)时,1+(c-1)x>cx.
【答案】(1)见解析;(2)见解析;(3)见解析
【解析】试题分析:(1)求出![]() ,在定义域内分别令
,在定义域内分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间; (2)原不等式等价于
的减区间; (2)原不等式等价于![]() ,运用(1)的单调性可得
,运用(1)的单调性可得![]() ,设
,设![]() ,求出单调性,即可得到
,求出单调性,即可得到![]() 成立;(3)设
成立;(3)设![]() ,求出导数,可令
,求出导数,可令![]() ,由
,由![]() , 可得
, 可得![]() ,由(1)可得
,由(1)可得![]() 有一解,设为
有一解,设为![]() 是
是![]() 的最小值点,运用最值,结合不等式的性质,即可得证,
的最小值点,运用最值,结合不等式的性质,即可得证,
试题解析:(1)解 由f (x)=ln x-x+1(x>0),得f ′(x)=![]() -1.
-1.
令f ′(x)=0,解得x=1.
当0<x<1时,f ′(x)>0,f (x)单调递增.
当x>1时,f ′(x)<0,f (x)单调递减.
因此f (x)在(0,1)上是增函数,在x∈(1,+∞)上为减函数.
(2)证明 由(1)知,函数f (x)在x=1处取得最大值f (1)=0.
∴当x≠1时,ln x<x-1.
故当x∈(1,+∞)时,ln x<x-1,ln![]() <
<![]() -1,即1<
-1,即1<![]() <x.
<x.
(3)证明 由题设c>1,设g(x)=1+(c-1)x-cx,
则g′(x)=c-1-cxln c.
令g′(x)=0,解得x0=![]() .
.
当x<x0时,g′(x)>0,g(x)单调递增;
当x>x0时,g′(x)<0,g(x)单调递减.
由(2)知1<![]() <c,故0<x0<1.
<c,故0<x0<1.
又g(0)=g(1)=0,故当0<x<1时,g(x)>0.
∴当x∈(0,1)时,1+(c-1)x>cx.


科目:高中数学 来源: 题型:
【题目】如图所示的几何体QPABCD为一简单组合体,在底面ABCD中,∠DAB=60°,AD⊥DC,AB⊥BC,QD⊥平面ABCD,PA∥QD,PA=1,AD=AB=QD=2.

(1)求证:平面PAB⊥平面QBC;
(2)求该组合体QPABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平面PAC⊥平面ABC,点E、F、O分别为线段PA、PB、AC的中点,点G是线段CO的中点,AB=BC=AC=4,PA=PC=2![]() .求证:
.求证:

(1)PA⊥平面EBO;
(2)FG∥平面EBO.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月23日“世界读书日”来临之际,某校为了了解中学生课外阅读情况,随机抽取了100名学生,并获得了他们一周课外阅读时间(单位:小时)的数据,按阅读时间分组:第一组[0,5), 第二组[5,10),第三组[10,15),第四组[15,20),第五组[20,25],绘制了频率分布直方图如下图所示。已知第三组的频数是第五组频数的3倍。
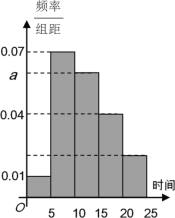
(1)求![]() 的值,并根据频率分布直方图估计该校学生一周课外阅读时间的平均值;
的值,并根据频率分布直方图估计该校学生一周课外阅读时间的平均值;
(2)现从第三、四、五这3组中用分层抽样的方法抽取6人参加校“中华诗词比赛”。经过比赛后,从这6人中随机挑选2人组成该校代表队,求这2人来自不同组别的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是![]() 的中点.
的中点.
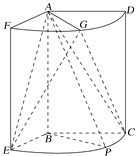
(1)设P是![]() 上的一点,且AP⊥BE,求∠CBP的大小;
上的一点,且AP⊥BE,求∠CBP的大小;
(2)当AB=3,AD=2时,求二面角E-AG-C的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)的定义域为(0,+∞),且对一切x>0,y>0都有![]() ,当
,当![]() 时,有
时,有![]()
(1)求f(1)的值;
(2)判断f(x)的单调性并加以证明;
(3)若f(4)=2,求f(x)在[1,16]上的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】气象意义上,从春季进入夏季的标志为:“连续5天的日平均温度不低于22℃”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数):
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体均值为24;
③丙地:5个数据的中有一个数据是32,总体均值为26,总体方差为10.8;
则肯定进入夏季的地区的有( )
A. ①②③ B. ①③ C. ②③ D. ①
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com