
| A. | $\frac{1}{{2\sqrt{e}}}$ | B. | $\frac{1}{{\sqrt{e}}}$ | C. | $\frac{1}{e}$ | D. | $\frac{1}{e^2}$ |
分析 先作出函数的图象,结合图象先判断x1,x2,x3的取值范围和对应关系.然后去判断$\frac{{f({x_3})}}{{{x_1}{x_2}^2}}$的最大值即可.
解答 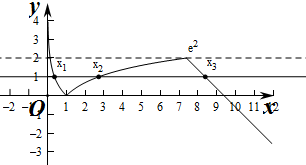 解:作出函数f(x)的图象如图:
解:作出函数f(x)的图象如图:
f(e2)=|lne2|=2,
当x>e2,由f(x)=e2+2-x=0得x=e2+2,
若f(x1)=f(x2)=f(x3),
则0<x1<1,1<x2<e2,e2<x3<2+e2,
由f(x1)=f(x2)得|lnx1|=|lnx2|,
即-lnx1=lnx2,则lnx1+lnx2=lnx1x2=0,即x1x2=1,
则$\frac{{f({x_3})}}{{{x_1}{x_2}^2}}$=$\frac{f({x}_{3})}{{x}_{2}}=\frac{f({x}_{2})}{{x}_{2}}$=$\frac{ln{x}_{2}}{{x}_{2}}$,
设g(x)=$\frac{lnx}{x}$,1<x<e2,
则g′(x)=$\frac{\frac{1}{x}•x-lnx}{{x}^{2}}=\frac{1-lnx}{{x}^{2}}$,
由g′(x)>0得1-lnx>0,得lnx<1,即,1<x<e,
由g′(x)<0得1-lnx<0,得lnx>1,即e<x<e2,
即当x=e时,g(x)取得极大值,同时也是最大值g(e)=$\frac{lne}{e}$=$\frac{1}{e}$,
即$\frac{{f({x_3})}}{{{x_1}{x_2}^2}}$=$\frac{ln{x}_{2}}{{x}_{2}}$的最大值是$\frac{1}{e}$,
故选:C.
点评 本题考查函数对数函数的图象与性质,以及根据函数与方程的关系求参数的取值范围问题.利用数形结合思想是解决这类问题的关键.


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案科目:高中数学 来源: 题型:选择题
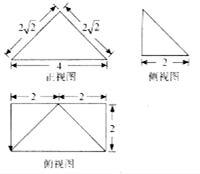 已知四棱锥P-ABCD的三视图如图所示,则此四棱锥外接球的半径为( )
已知四棱锥P-ABCD的三视图如图所示,则此四棱锥外接球的半径为( )| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | f′(3)<f′(4)<f(4)-f(3)<0 | B. | f′(3)<f(4)-f(3)<f′(4)<0 | C. | f′(4)<f(4)-f(3)<f′(3)<0 | D. | f(4)-f(3)<f′(4)<f′(3)<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 16 | B. | 8$\sqrt{6}$+6$\sqrt{2}$ | C. | 16$\sqrt{6}$ | D. | 16+6$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
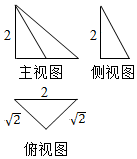
| A. | $\frac{9π}{2}$ | B. | $\frac{27π}{8}$ | C. | 36π | D. | 8π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,网格纸上小正方形的边长为1,粗实线画出的是某空间几何体的三视图,则该几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某空间几何体的三视图,则该几何体的表面积为( )| A. | 52 | B. | 34+9$\sqrt{2}$ | C. | 64 | D. | 34+8$\sqrt{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com