
甲、乙两人玩一种游戏;在装有质地、大小完全相同,编号分别为1,2,3,4,5,6六个球的口袋中,甲先模出一个球,记下编号,放回后乙再模一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
(1)求甲赢且编号和为8的事件发生的概率;
(2)这种游戏规则公平吗?试说明理由.
(1)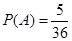 ;(2)这种游戏规则是公平的.
;(2)这种游戏规则是公平的.
解析试题分析:(1)设“两个编号和为8”为事件A,计算甲、乙两人取出的数字等可能的结果数,事件A包含的基本事件为(2,6),(3,5),(4,4),(5,3),(6,2)共5个,按古典概型概率的计算公式计算;
(2)首先按古典概型计算两人分别获胜的概率,通过比较大小,作出结论.
所以这种游戏规则是公平的.
试题解析:(1)设“两个编号和为8”为事件A,则事件A包含的基本事件为(2,6),(3,5),(4,4),(5,3),(6,2)共5个,又甲、乙两人取出的数字共有6×6=36(个)等可能的结果,
故
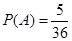 6分
6分
(2)这种游戏规则是公平的. 7分
设甲胜为事件B,乙胜为事件C,则甲胜即两编号和为偶数所包含的基本事件数有18个:(1,1),(1,3),(1,5),(2,2),(2,4),(2,6),(3,1),(3,3),(3,5),(4,2),(4,4),(4,6),(5,1),(5,3),(5,5),(6,2),(6,4),(6,6)
所以甲胜的概率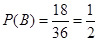 ,乙胜的概率
,乙胜的概率 =
=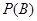 11分
11分
所以这种游戏规则是公平的. 12分
考点:古典概型概率的计算.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:解答题
一个布袋里有3个红球,2个白球共5个球. 现抽取3次,每次任意抽取2个,并待放回后再抽下一次.求:
(1)3次抽取中,每次取出的2个球都是1个白球和1个红球的概率;
(2)3次抽取中,有2次取出的2个球是1个白球和1个红球,还有1次取出的2个球同色的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)将一颗骰子先后抛掷2次,观察向上的点数,求:
(1)两数之和为6的概率;
(2)两数之积是6的倍数的概率;
(3)以第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=15的内部的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
有甲、乙两个班进行数学考试,按照大于或等于85分为优秀,85分以下为非优秀统计成绩后,得到如下的2×2列联表:
| | 优秀 | 非优秀 | 总计 |
| 甲班 | 20 | | |
| 乙班 | | 60 | |
| 总计 | | | 210 |
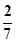 .
. ,其中
,其中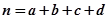 .
.| 参考数据 | 当 ≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; ≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
当 >2.706时,有90%的把握判定变量A,B有关联; >2.706时,有90%的把握判定变量A,B有关联; | |
当 >3.841时,有95%的把握判定变量A,B有关联; >3.841时,有95%的把握判定变量A,B有关联; | |
当 >6.635时,有99%的把握判定变量A,B有关联. >6.635时,有99%的把握判定变量A,B有关联. |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某中学在运动会期间举行定点投篮比赛,规定每人投篮4次,投中一球得2分,没有投中得0分,假设每次投篮投中与否是相互独立的,已知小明每次投篮投中的概率都是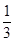 .
.
(1)求小明在投篮过程中直到第三次才投中的概率;
(2)求小明在4次投篮后的总得分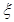 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如下表所示: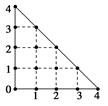
| X | 1 | 2 | 3 | 4 |
| Y | 51 | 48 | 45 | 42 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(满分14分)随机将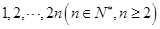 这2n个连续正整数分成A,B两组,每组n个数,A组最小数为
这2n个连续正整数分成A,B两组,每组n个数,A组最小数为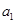 ,最大数为
,最大数为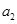 ;B组最小数为
;B组最小数为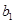 ,最大数为
,最大数为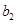 ,记
,记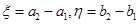
(1)当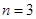 时,求
时,求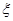 的分布列和数学期望;
的分布列和数学期望;
(2)令C表示事件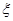 与
与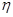 的取值恰好相等,求事件C发生的概率
的取值恰好相等,求事件C发生的概率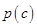 ;
;
(3)对(2)中的事件C,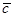 表示C的对立事件,判断
表示C的对立事件,判断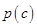 和
和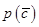 的大小关系,并说明理由。
的大小关系,并说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com