
分析 (1)设“两个班级的同学都至少胜一场”为事件A,其对立事件为:一班3场都胜或3场都输了,利用P(A)=1-P($\overline{A}$)即可得出.
(2)设一班获胜场数为X,由题意可得:X=0,1,2,3.利用相互独立与互斥事件的概率计算公式即可得出.
解答 解:(1)设“两个班级的同学都至少胜一场”为事件A,
则P(A)=1-P($\overline{A}$)=1-[$\frac{3}{4}×\frac{1}{2}×\frac{1}{4}$+(1-$\frac{3}{4}$)×(1-$\frac{1}{2}$)×(1-$\frac{1}{4}$)]=$\frac{13}{16}$.
(2)设一班获胜场数为X,由题意可得:X=0,1,2,3.
P(X=0)=(1-$\frac{3}{4}$)×(1-$\frac{1}{2}$)×(1-$\frac{1}{4}$)=$\frac{3}{32}$,
P(X=1)=$\frac{3}{4}$×(1-$\frac{1}{2}$)×(1-$\frac{1}{4}$)+(1-$\frac{3}{4}$)×$\frac{1}{2}$×(1-$\frac{1}{4}$)+(1-$\frac{3}{4}$)×(1-$\frac{1}{2}$)×$\frac{1}{4}$=$\frac{13}{32}$,
P(X=3)=$\frac{3}{4}$×$\frac{1}{2}$×$\frac{1}{4}$=$\frac{3}{32}$.P(X=2)=1-P(X=0)-P(X=1)-P(X=3)=$\frac{13}{32}$.
其分布列为:x的分布列为
| x | 0 | 1 | 2 | 3 |
| P | $\frac{3}{32}$ | $\frac{13}{32}$ | $\frac{13}{32}$ | $\frac{3}{32}$ |
点评 本题考查了古典概率计算公式、相互独立、对立与互斥事件的概率计算公式、分布列及其数学期望,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
 某加油站工作人员根据以往该加油站的销售情况,绘制了该加油站日销售量的频率分布直方图,如图所示:
某加油站工作人员根据以往该加油站的销售情况,绘制了该加油站日销售量的频率分布直方图,如图所示:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
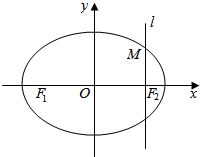 如图,在直角坐标系xOy中,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1和F2.过右焦点为F2且与x轴垂直的直线l与椭圆C相交,其中一个交点为M(1,$\frac{3}{2}$).(1)求椭圆C的方程:
如图,在直角坐标系xOy中,设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右两个焦点分别为F1和F2.过右焦点为F2且与x轴垂直的直线l与椭圆C相交,其中一个交点为M(1,$\frac{3}{2}$).(1)求椭圆C的方程:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,1) | B. | ($\frac{1}{2}$,2) | C. | (1,$\frac{3}{2}$) | D. | (1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | [-1,1] | C. | [-2,2] | D. | [0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{5}{12}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com