Question

若二次函数f(x)＝ax²＋bx＋c(a≠0)满足f(x＋1)－f(x)＝2x，且f(0)＝1.

(1)求f(x)的解析式；

(2)若在区间[－1,1]上，不等式f(x)>2x＋m恒成立，求实数m的取值范围．

 

Answer 1

【答案】

(1) f(x)＝x²－x＋1.(2) (－∞，－1)．

【解析】

试题分析：(1)由f(0)＝1得，c＝1.                     1分

∴f(x)＝ax²＋bx＋1.又f(x＋1)－f(x)＝2x，

∴a(x＋1)²＋b(x＋1)＋1－(ax²＋bx＋1)＝2x，

即2ax＋a＋b＝2x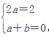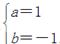，∴∴        5分

因此，f(x)＝x²－x＋1.

(2)f(x)>2x＋m等价于x²－x＋1>2x＋m，                 6分

即x²－3x＋1－m>0，要使此不等式在[－1,1]上恒成立，

只需使函数g(x)＝x²－3x＋1－m在[－1,1]上的最小值大于0即可．   8分

∵g(x)＝x²－3x＋1－m在[－1,1]上单调递减，

∴g(x)_min＝g(1)＝－m－1，                                10分

由－m－1>0得，m<－1.

因此满足条件的实数m的取值范围是(－∞，－1)．          12分

考点：本题考查了一元二次函数及其恒成立问题

点评：对于二次函数f(x)=ax²+bx+c=0(a≠0)在实数集R上恒成立问题可利用判别式直接求解，即：f(x)>0恒成立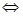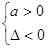；f(x)<0恒成立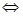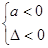，若是二次函数在指定区间上的恒成立问题，还可以利用韦达定理以及根与系数的分布知识求解