
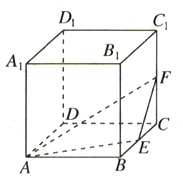
【题目】如图所示,在棱长为1的正方体![]() 中,点
中,点![]() 分别是棱
分别是棱![]() 的中点,
的中点,![]() 是侧面
是侧面![]() 内一点,若
内一点,若![]() 平面
平面![]() ,则线段
,则线段![]() 长度的取值范围是( )
长度的取值范围是( )
A.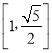 B.
B.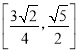 C.
C.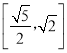 D.
D.![]()
【答案】B
【解析】
分别取棱BB1、B1C1的中点M、N,连接MN,易证平面A1MN∥平面AEF,由题意知点P必在线段MN上,由此可判断P在M或N处时A1P最长,位于线段MN中点处时最短,通过解直角三角形即可.
如图所示:分别取棱BB1、B1C1的中点M、N,连接MN,连接BC1,
∵M、N、E、F为所在棱的中点,∴MN∥BC1,EF∥BC1,
∴MN∥EF,又MN平面AEF,EF平面AEF,∴MN∥平面AEF;
∵AA1∥NE,AA1=NE,∴四边形AENA1为平行四边形,
∴A1N∥AE,又A1N平面AEF,AE平面AEF,∴A1N∥平面AEF,
又A1N∩MN=N,∴平面A1MN∥平面AEF,∵P是侧面BCC1B1内一点,且A1P∥平面AEF,
则P必在线段MN上,在Rt△A1B1M中,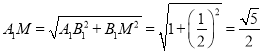 ,
,
同理,在Rt△A1B1N中,求得A1N=![]() ,∴△A1MN为等腰三角形,
,∴△A1MN为等腰三角形,
当P在MN中点O时A1P⊥MN,此时A1P最短,P位于M、N处时A1P最长,
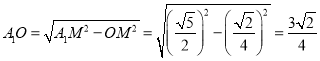 ,A1M=A1N=
,A1M=A1N=![]() ,
,
所以线段A1P长度的取值范围是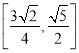 .
.
故选B.


科目:高中数学 来源: 题型:
【题目】为了适应高考改革,某中学推行“创新课堂”教学.高一平行甲班采用“传统教学”的教学方式授课,高一平行乙班采用“创新课堂”的教学方式授课,为了比较教学效果,期中考试后,分别从两个班中各随机抽取![]() 名学生的成绩进行统计分析,结果如下表:(记成绩不低于
名学生的成绩进行统计分析,结果如下表:(记成绩不低于![]() 分者为“成绩优秀”)
分者为“成绩优秀”)
分数 |
|
|
|
|
|
|
|
甲班频数 |
|
|
|
|
|
|
|
乙班频数 |
|
|
|
|
|
|
|
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断是否有
列联表,并判断是否有![]() 以上的把握认为“成绩优秀与教学方式有关”?
以上的把握认为“成绩优秀与教学方式有关”?
甲班 | 乙班 | 总计 | |
成绩优秀 | |||
成绩不优秀 | |||
总计 |
(Ⅱ)现从上述样本“成绩不优秀”的学生中,抽取![]() 人进行考核,记“成绩不优秀”的乙班人数为
人进行考核,记“成绩不优秀”的乙班人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
参考公式:![]() ,其中
,其中![]() .
.
临界值表
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汉诺塔(又称河内塔)问题是源于印度一个古老传说的益智玩具大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上.并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘.如下图所示,从左到右有ABC三根柱子,其中A柱子上面有从小叠到大的n个圆盘,现要求将A柱子上的圆盘移到C柱子上去,期间只有一个原则:一次只能移动一个盘子且大盘子不能在小盘子上面,则移动的次数为_______(用![]() 表示)
表示)
A B
B C
C
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,椭圆![]() 与一等轴双曲线相交,
与一等轴双曲线相交,![]() 是其中一个交点,并且双曲线的顶点是该椭圆的焦点
是其中一个交点,并且双曲线的顶点是该椭圆的焦点![]() ,
,![]() ,双曲线的焦点是椭圆的左、右顶点,设
,双曲线的焦点是椭圆的左、右顶点,设![]() 为该双曲线上异于顶点的任意一点,直线
为该双曲线上异于顶点的任意一点,直线![]() 的斜率分别为
的斜率分别为![]() ,且直线
,且直线![]() 和
和![]() 与椭圆的交点分别为
与椭圆的交点分别为![]() 、
、![]() 和
和![]() 、
、![]() .
.

(1)求椭圆和双曲线的标准方程;
(2)(i)证明:![]() ;
;
(ii)是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn,且满足Sn+n=2an(n∈N*).
(1)证明:数列{an+1}为等比数列,并求数列{an}的通项公式;
(2)若bn=(2n+1)an+2n+1,数列{bn}的前n项和为Tn.求满足不等式![]() >2010的n的最小值.
>2010的n的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在直角梯形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 上的点,
上的点,![]() ,且
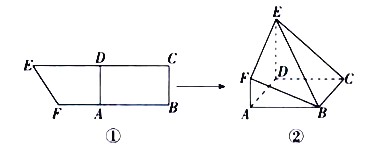
,且![]() (①).将四边形
(①).将四边形![]() 沿
沿![]() 折起,连接
折起,连接![]() (②).在折起的过程中,下列说法中正确的是( )
(②).在折起的过程中,下列说法中正确的是( )
A.![]() 平面
平面![]()
B.![]() 四点不可能共面
四点不可能共面
C.若![]() ,则平面
,则平面![]() 平面
平面![]()
D.平面![]() 与平面
与平面![]() 可能垂直
可能垂直
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com