
����Ŀ��2017��5��14��,��һ�조һ��һ·�����ʸ߷���̳�ڱ�������,Ϊ�˽ⲻͬ������˶ԡ�һ��һ·����ע�̶�,ij���������ȡ��������15-75��֮���100�˽��е���, ��ͳ�ơ������ꡱ�롰�����ꡱ������֮��Ϊ9:11
��ע | ����ע | �ϼ� | |
������ | 15 | ||
������ | |||
�ϼ� | 50 | 50 | 100 |
(1)������֪������������![]() �����������ж��ܷ���
�����������ж��ܷ���![]() �İ�����Ϊ��ע��һ��һ·���Ƿ��������йأ�
�İ�����Ϊ��ע��һ��һ·���Ƿ��������йأ�
(2)�ִӳ�ȡ���������в��÷ֲ�����İ취ѡȡ9�˽����ʾ�����.����9������ѡȡ3�˽��������ѯ��,��ѡȡ��3���й�ע��һ��һ·��������ΪX,��X�ķֲ��м���ѧ����.
��:�ο���ʽ ������
������![]()
�ٽ�ֵ����
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
���𰸡�(1) ��![]() �İ�����Ϊ��ע��һ��һ·�� ��������й�(2)
�İ�����Ϊ��ע��һ��һ·�� ��������й�(2) ![]()
�����������������(1)���������![]() ������������
������������![]() �������ٽ�ֵ�ó�������(2)���ݷֲ���������ó��������
�������ٽ�ֵ�ó�������(2)���ݷֲ���������ó��������![]() �Ŀ���ȡֵ�������Ӧ�ĸ���ֵ��д��
�Ŀ���ȡֵ�������Ӧ�ĸ���ֵ��д��![]() �ķֲ��У��������ѧ����ֵ.
�ķֲ��У��������ѧ����ֵ.
���������(1)�������֪,��ȡ����������������![]() ��,��������������
��,��������������![]() ��.
��.
��ɵ�2��2�������磺
��ע | ����ע | �ϼ� | |
������ | 15 | 30 | 45 |
������ | 35 | 20 | 55 |
�ϼ� | 50 | 50 | 100 |
��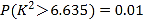
��Ϊ![]() ��
�� ![]() ��������
��������![]() �İ�����Ϊ��ע��һ��һ·�� ��������й�
�İ�����Ϊ��ע��һ��һ·�� ��������й�
(2)��������֪,ѡ����ע������Ϊ3,����ע������Ϊ6,����9������ѡȡ3�˽��������ѯ��, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
| 0 | 1 | 2 | 3 |
|
|
|
|
|
����![]() �ķֲ���Ϊ��ѧ����
�ķֲ���Ϊ��ѧ����![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijֲ������һ���������������Թݣ�������ABEΪ���չʾ������AB��AE�����ͳ��ȣ��ı���BCDE����������������BCD=��CDE=120�㣬��BAE=60�㣬DE=3BC=3CD=![]() �ס�
�ס�
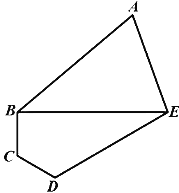
(1)��������߽�BE�ij��ȣ�
(2)������ABEΪ��������Σ�����ͳ����ܳ���AB+AE��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��������b��������c���������ɼӷ�ԭ�����˷�ԭ������1�������1��������ȡ�����ɸ��������ȡ�����ɣ�1+a����1+b����չ��ʽ1+a+b+ab��ʾ�������磺��1����ʾһ����ȡ����a����ʾȡ��һ��������ab�����ʾ�Ѻ��������ȡ�������Դ����ƣ����и�ʽ�У���չ��ʽ��������ʾ��5��������ĺ���5�������������5��������ĺ�����ȡ�����ɸ��������е�����ȡ����ȡ��������ȡ�����ǣ�������
A.��1+a+a2+a3+a4+a5����1+b5����1+c��5
B.��1+a5����1+b+b2+b3+b4+b5����1+c��5
C.��1+a��5��1+b+b2+b3+b4+b5����1+c5��
D.��1+a5����1+b��5��1+c+c2+c3+c4+c5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��
�� ![]() ����֪
����֪![]() ��
��![]() ��
��![]() ������ͬ������.
������ͬ������.
��1����![]() ��
�� ![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����![]() ��
��![]() �ϵ���Сֵ��
�ϵ���Сֵ��
��3������![]() ��
�� ![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����P-ABCD�ĵ���ABCD��ƽ���ı��Σ�PA��ƽ��ABCD��M��AD���е㣬N��PC���е㣮
��1����֤��MN��ƽ��PAB��
��2����ƽ��PMC��ƽ��PAD����֤��CM��AD��
��3����ƽ��ABCD�Ǿ��Σ�PA=AB����֤��ƽ��PMC��ƽ��PBC��
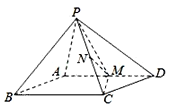
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������һ��U��ˮ��PABQ����A=��B=90��������һ���̰ӣ�E��AP�ϣ�N��BQ�ϣ���Χ��һ���������EABN��������ֲˮ��ֲ�Ϊ�����������������AB�ϵ�M���ֱ����E��N��2���ָ���ME��MN������Χ����ֳ�3�����֣���ͼ����ÿ������ֲ��ͬ��ˮ��ֲ���֪AB=a��EM=BM����MEN=90�����������ָ����ܳ���Ϊl��
��1�����AME=2������������ʾ��l��������ʽ����д��������
��2����l����Сֵ��
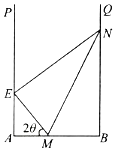
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ABC�������ڽ�A��B��C���Եı߷ֱ�Ϊa��b��c����֪sin![]() ��
��
�������A�Ĵ�С��
������a=2����b+c�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij��������4ǧ�߿շ��У��Ӿ���½��A��ˮƽ����10ǧ�״���ʼ�½�����֪�½����й켣Ϊij���κ���ͼ���һ���֣���ú����Ľ���ʽΪ�� �� 
A.y= ![]() ��
�� ![]() x
x
B.y= ![]() x3��
x3�� ![]() x
x
C.y= ![]() x3��x
x3��x
D.y=�� ![]() x3+
x3+ ![]() x
x
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���֪Բ
�У���֪Բ![]() ��
��![]() ��Բ
��Բ![]() ��
��![]()
![]() ��
��![]() ����
����![]() ��.
��.
��1����![]() Ϊ�������ϵĵ㣬���㣺����P�ֱ���Բ
Ϊ�������ϵĵ㣬���㣺����P�ֱ���Բ![]() ��Բ
��Բ![]() ��һ�����ߣ��е�ֱ�Ϊ
��һ�����ߣ��е�ֱ�Ϊ![]() ��
��![]() ��ʹ��
��ʹ��![]() ��������������������ĵ�
��������������������ĵ�![]() �����ꣻ
�����ꣻ
��2����б��Ϊ������ֱ��![]() ƽ��Բ
ƽ��Բ![]() ����֤��ֱ��
����֤��ֱ��![]() ��Բ
��Բ![]() ���ཻ.
���ཻ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com