
| A. | 点在圆上 | B. | 点在圆内 | C. | 点在圆外 | D. | 都有可能 |
分析 由已知得圆心(0,0)到直线ax+by-1=0的距离d<1,从而a2+b2>1,从而得到点(a,b)到圆心(0,0)的距离d′>1=r,由此能判断点(a,b)与此圆的位置关系.
解答 解:∵直线ax+by=1经过圆x2+y2=1内一点,
∴圆心(0,0)到直线ax+by-1=0的距离d=$\frac{|-1|}{\sqrt{{a}^{2}+{b}^{2}}}$<1,
∴a2+b2>1,
∴点(a,b)到圆心(0,0)的距离d′=$\sqrt{{a}^{2}+{b}^{2}}$>1=r,
∴点(a,b)与此圆的位置关系是点在圆外.
故选:C.
点评 本题考查点与圆的位置关系的判断,是基础题,解题时要认真审题,注意点到直线距离公式和两点间距离公式的合理运用.


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$$\overrightarrow{AB}$+$\frac{1}{3}\overrightarrow{OB}$+$\frac{1}{3}\overrightarrow{OC}$ | B. | $\frac{1}{4}$($\overline{OA}+\overline{OB}+\overrightarrow{OC}$) | C. | $\frac{1}{3}$($\overline{OA}+\overline{OB}+\overrightarrow{OC}$) | D. | $\frac{1}{3}$$\overrightarrow{OA}+\frac{1}{6}\overrightarrow{OB}+\frac{1}{3}\overrightarrow{OC}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {2,3} | C. | {2,3,4} | D. | {1,2,3,4,6} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
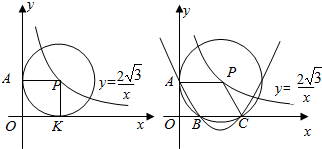 在直角坐标系xOy中,已知点P是反比例函数y=$\frac{2\sqrt{3}}{x}$(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.
在直角坐标系xOy中,已知点P是反比例函数y=$\frac{2\sqrt{3}}{x}$(x>0)图象上一个动点,以P为圆心的圆始终与y轴相切,设切点为A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com