
【题目】一条光线从点A(3,2)发出,经x轴反射后,通过点B(-1,6),求入射光线和反射光线所在的直线方程.
【答案】解如图所示,作A点关于x轴的对称点A′,显然,A′坐标为(3,-2),连接A′B,则A′B所在直线即为反射光线.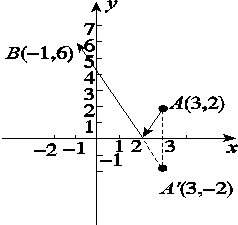
由两点式可得直线A′B的方程为 ![]() ,即2x+y-4=0.
,即2x+y-4=0.
同理,点B关于x轴的对称点为B′(-1,-6),
由两点式可得直线AB′的方程为 ![]() ,即2x-y-4=0,
,即2x-y-4=0,
∴入射光线所在直线方程为2x-y-4=0,
反射光线所在直线方程为2x+y-4=0:
【解析】由光在反射过程中,入射光线与反射光线关于x轴对称,求出点A,B关于x轴的对称点的坐标,即求出了入射光线与反射光线分别过两点,则两点式方程求出直线方程.
【考点精析】利用两点式方程对题目进行判断即可得到答案,需要熟知直线的两点式方程:已知两点![]() 其中
其中![]() 则:y-y1/y-y2=x-x1/x-x2.
则:y-y1/y-y2=x-x1/x-x2.


 教学练新同步练习系列答案
教学练新同步练习系列答案科目:高中数学 来源: 题型:
【题目】已知f(x)=x2+bx+c为偶函数,曲线y=f(x)过点(2,5),g(x)=(x+a)f(x).
(1)求曲线y=g(x)有斜率为0的切线,求实数a的取值范围;
(2)若当x=﹣1时函数y=g(x)取得极值,确定y=g(x)的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为  (t为参数),再以原点为极点,以x轴正半轴为极轴建立坐标系,并使得它与直角坐标系有相同的长度单位,在该极坐标系中圆C的方程为ρ=4sinθ.
(t为参数),再以原点为极点,以x轴正半轴为极轴建立坐标系,并使得它与直角坐标系有相同的长度单位,在该极坐标系中圆C的方程为ρ=4sinθ.
(1)求圆C的直角坐标方程;
(2)设圆C与直线l交于点A,B,若点M的坐标为(﹣2,1),求|MA|+|MB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经问卷调查,某班学生对摄影分别执“喜欢”“不喜欢”和“一般”三种态度,其中执“一般”态度的比“不喜欢”的多12人,按分层抽样方法从全班选出部分学生座谈摄影,如果选出的是5位“喜欢”摄影的同学、1位“不喜欢”摄影的同学和3位执“一般”态度的同学,那全班学生中“喜欢”摄影的比全班学生人数的一半还多人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ ![]() (x>0)过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N,设g(t)=|MN|,若对任意的正整数n,在区间[2,n+
(x>0)过点P(1,0)作曲线y=f(x)的两条切线PM,PN,切点分别为M,N,设g(t)=|MN|,若对任意的正整数n,在区间[2,n+ ![]() ]内,若存在m+1个数a1 , a2 , …am+1 , 使得不等式g(a1)+g(a2)+…g(am)<g(am+1),则m的最大值为( )
]内,若存在m+1个数a1 , a2 , …am+1 , 使得不等式g(a1)+g(a2)+…g(am)<g(am+1),则m的最大值为( )
A.5
B.6
C.7
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com