
【题目】已知函数![]() ,若存在实数
,若存在实数![]() 使得不等式
使得不等式![]() 成立,求实数
成立,求实数![]() 的取值范围为( )
的取值范围为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
【答案】A
【解析】解:对函数求导可得: ![]() ,
,
且: ![]() ,
,
![]() ,则导函数
,则导函数![]() 单调递增,而
单调递增,而![]() ,
,
故![]() ,
,
由存在性的条件可得关于实数![]() 的不等式:
的不等式: ![]() ,
,
解得: ![]() .
.
本题选择D选项.
本题首先求解函数的解析式,然后结合函数的最值转化即可.
求函数最值的常用方法:
(1)单调性法:先确定函数的单调性,再由单调性求最值;
(2)图象法:先作出函数的图象,再观察其最高点、最低点,求出最值;
(3)基本不等式法:先对解析式变形,使之具备“一正二定三相等”的条件后用基本不等式求出最值;
(4)导数法:先求导,然后求出在给定区间上的极值,最后结合端点值,求出最值;
(5)换元法:对比较复杂的函数可通过换元转化为熟悉的函数,再用相应的方法求最值.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】学校为了了解高三学生每天自主学习中国古典文学的时间,随机抽取了高三男生和女生各50名进行问卷调查,其中每天自主学习中国古典文学的时间超过3小时的学生称为“古文迷”,否则为“非古文迷”,调查结果如表:
古文迷 | 非古文迷 | 合计 | |
男生 | 26 | 24 | 50 |
女生 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据表中数据判断能否有![]() 的把握认为“古文迷”与性别有关?
的把握认为“古文迷”与性别有关?
(2)先从调查的女生中按分层抽样的方法抽出5人进行理科学习时间的调查,求所抽取的5人中“古文迷”和“非古文迷”的人数;
(3)现从(2)中所抽取的5人中再随机抽取3人进行体育锻炼时间的调查,记这3人中“古文迷”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列与数学期望.
的分布列与数学期望.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.321 | 3.841 | 5.024 | 6.635 |
参考公式: 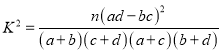 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,以
两点,以![]() 为对角线作正方形
为对角线作正方形![]() ,记直线
,记直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,问
,问![]() 、
、![]() 两点间距离是否为定值?如果是,求出定值;如果不是,请说明理由.
两点间距离是否为定值?如果是,求出定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某校组织的“共筑中国梦”竞赛活动中,甲、乙两班各有6名选手参赛,在第一轮笔试环节中,评委将他们的笔试成绩作为样本数据,绘制成如图所示的茎叶图,为了增加结果的神秘感,主持人故意没有给出甲、乙两班最后一位选手的成绩,只是告知大家,如果某位选手的成绩高于90分(不含90分),则直接“晋级”.
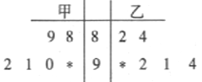
(1)求乙班总分超过甲班的概率;
(2)主持人最后宣布:甲班第六位选手的得分是90分,乙班第六位选手的得分是97分,
①请你从平均分和方差的角度来分析两个班的选手的情况;
②主持人从甲乙两班所有选手成绩中分别随机抽取2个,记抽取到“晋级”选手的总人数为![]() ,求
,求![]() 的分
的分
布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某省电视台为了解该省卫视一档成语类节目的收视情况,抽查东西两部各个城市,得到观看该节目的人数(单位:千人),如茎叶图所示,其中一个数字被污损.
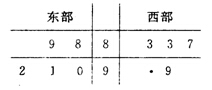
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率;
(2)随着节目的播出,极大激发了观众对成语知识学习积累的热情,从中获益匪浅.现从观看该节目的观众中随机统计了位观众的周均学习成语知识的时间(单位:小时)与年龄(单位:岁),并制作了对照表(如下表所示),
年龄x(岁) | ||||
周均学习成语知识时间y(小时) |
由表中数据,试求线性回归方程,并预测年龄为岁观众周均学习成语知识时间.
参考公式: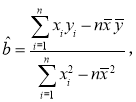 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某教研机构随机抽取某校20个班级,调查各班关注汉字听写大赛的学生人数,根据所得数据的茎叶图,以组距为5将数据分组成![]() 时,所作的频率分布直方图如图所示,则原始茎叶图可能是( )
时,所作的频率分布直方图如图所示,则原始茎叶图可能是( )
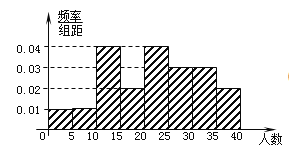
A.  B.
B. 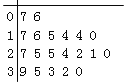
C. 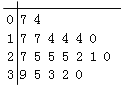 D.
D. 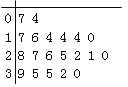
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,右焦点
,右焦点![]() ,过点
,过点 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,求证:
,求证: ![]() 三点共线;
三点共线;
(3) 当![]() 面积最大时,求直线
面积最大时,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com