【题目】根据以往的经验，某建筑工程施工期间的降水量
（单位：
）对工期的影响如下表：
降水量 |
|
|
|
|
工期延误天数 | 0 | 1 | 3 | 6 |
根据某气象站的资料，某调查小组抄录了该工程施工地某月前
天的降水量的数据，绘制得到降水量的折线图，如下图所示.
（1）求这天的平均降水量；
（2）根据降水量的折线图，分别估计该工程施工延误天数
的概率.
科目：高中数学 来源： 题型：
【题目】绝对值|x﹣1|的几何意义是数轴上的点x与点1之间的距离，那么对于实数a，b，
的几何意义即为点x与点a、点b的距离之和.
（1）直接写出
与
的最小值，并写出取到最小值时x满足的条件；
（2）设a1≤a2≤…≤an是给定的n个实数，记S=
.试猜想：若n为奇数，则当x∈ 时S取到最小值；若n为偶数，则当x∈ 时，S取到最小值；（直接写出结果即可）
（3）求
的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】选修4-4：坐标系与参数方程
在极坐标系中，曲线
，
，C与l有且仅有一个公共点．
（Ⅰ）求a；
（Ⅱ）O为极点，A，B为C上的两点，且
，求
的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设
为常数，函数
，给出以下结论：
（1）若
，则
存在唯一零点
（2）若
，则
（3）若有两个极值点
，则
其中正确结论的个数是（ ）
A. 3B. 2C. 1D. 0
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某学校在九年级上学期开始时要掌握全年级学生每分钟跳绳的情况，随机抽取了100名学生进行测试，得到频率分布直方图（如图），且规定计分规则如下表：
每分钟跳绳个数 |
|
|
|
|
得分 | 17 | 18 | 19 | 20 |
（1）请估计学生的跳绳个数的众数和平均数（保留整数）；
（2）若从跳绳个数在
，
两组中按分层抽样的方法抽取9人参加正式测试，并从中任意选取2人，求2人得分之和不大于34分的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】根据以往的经验，某建筑工程施工期间的降水量
（单位：
）对工期的影响如下表：
降水量 |
|
|
|
|
工期延误天数 | 0 | 1 | 3 | 6 |
根据某气象站的资料，某调查小组抄录了该工程施工地某月前
天的降水量的数据，绘制得到降水量的折线图，如下图所示.
（1）根据降水量的折线图，分别求该工程施工延误天数
的频率；
（2）以（1）中的频率作为概率，求工期延误天数
的分布列及数学期望与方差.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图1,在正方形
中，
是
的中点，点
在线段
上,且
.若将
分别沿
折起，使
两点重合于点
,如图2.
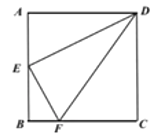
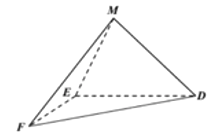
图1 图2
(1)求证:
平面
；
(2)求直线
与平面
所成角的正弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知f（x）是R上的奇函数，且x>0时，f（x）=x2-4x+3．
求：（1）f（x）的解析式．
（2）已知t＞0，求函数f（x）在区间[t，t+1]上的最小值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
