练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】端午节是我国民间为纪念爱国诗人屈原的一个传统节日.某市为了解端午节期间粽子的销售情况，随机问卷调查了该市1000名消费者在去年端午节期间的粽子购买量（单位：克），所得数据如下表所示：

    购买量

    人数

    100

    300

    400

    150

    50

    将烦率视为概率

    （1）试求消费者粽子购买量不低于300克的概率；

    （2）若该市有100万名消费者，请估计该市今年在端午节期间应准备多少千克棕子才能满足市场需求（以各区间中点值作为该区间的购买量）.

    【答案】（1）（2）225000千克

    【解析】

    （1）由表得粽子购买量不低于300克的共有200人，可得其概率；

    （2）先计算出每位顾客粽子购买量的平均数，再乘100万即可.

    （1）在随机调查的该超市1000名消费者中，

    粽子购买量不低于300克的共有200人，

    所以消费者粽子购买量不低于300克的概率

    （2）由题意可得，购买的概率为0.1，购买的概率为0.3，购买的概率为0.4，购买[300，400）的概率为0.15，购买的概率为0.05

    所以粽子购买量的平均数为克

    所以需准备粽子的重量为0.225×106=225000千克

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，矩形ABCD中，，，是AD的中点，将沿BE翻折，记为，在翻折过程中，①点在平面BCDE的射影必在直线AC上；②记和与平面BCDE所成的角分别为，，则的最大值为0；③设二面角的平面角为，则.其中正确命题的个数是（ ）

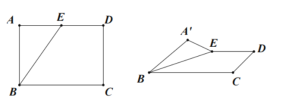
    A.0B.1C.2D.3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知梯形ABCD满足AB∥CD，∠BAD＝45°，以A，D为焦点的双曲线Γ经过B，C两点.若CD＝7AB，则双曲线Γ的离心率为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）若，求的最值；

    （2）若当时，，求m的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，证明：；

    （2）当时，讨论函数的零点个数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校的一个社会实践调查小组，在对该校学生的良好“用眼习惯”的调查中，随机发放了120分问卷.对收回的100份有效问卷进行统计，得到如下列联表：

    做不到科学用眼

    能做到科学用眼

    合计

    男

    45

    10

    55

    女

    30

    15

    45

    合计

    75

    25

    100

    （1）现按女生是否能做到科学用眼进行分层，从45份女生问卷中抽取了6份问卷，从这6份问卷中再随机抽取3份，并记其中能做到科学用眼的问卷的份数，试求随机变量的分布列和数学期望；

    （2）若在犯错误的概率不超过的前提下认为良好“用眼习惯”与性别有关，那么根据临界值表，最精确的的值应为多少？请说明理由.

    附：独立性检验统计量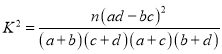，其中.

    独立性检验临界值表：

    0.25

    0.15

    0.10

    0.05

    0.025

    1.323

    2.072

    2.706

    3.840

    5.024

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某中学某社团为研究高三学生课下钻研数学时间与数学考试中的解答题得分的关系，随机调查了某中学高三某班名学生每周课下钻研数学时间(单位：小时)与高三下学期期中考试数学解答题得分，数据如下表：

    2

    4

    6

    8

    10

    12

    30

    38

    44

    48

    50

    54

    （1）根据上述数据，求出数学考试中的解答题得分与该学生课下钻研数学时间的线性回归方程，并预测某学生每周课下钻研数学时间为小时其数学考试中的解答题得分；

    （2）从这人中任选人，求人中至少有人课下钻研数学时间不低于小时的概率.

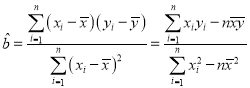    参考公式：，其中， ；参考数据：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某运输公司每天至少向某地运送物质，该公司有8辆载重为的型卡车与4辆载重为的型卡车，有10名驾驶员，每辆卡车每天往返的次数为型卡车4次，型卡车3次；每辆卡车每天往返的成本为型卡车320元，型卡车504元，你认为该公司怎样调配车辆，使运费成本最低，最低运费是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】是否存在常数a，b，c，使等式N+都成立，并证明你的结论.

    查看答案和解析>>

    同步练习册答案