【题目】某车间为了规定工时定额，需要确定加个某零件所花费的时间，为此作了四次实验，得到的数据如下：
零件的个数x（个） | 2 | 3 | 4 | 5 |
加工的时间y（小时） | 2.5 | 3 | 4 | 4.5 |
（1）求出y关于x的线性回归方程；
（2）试预测加工10个零件需要多少时间？
【答案】
（1）解：由表中数据得： 
xiyi=52.5， 
=3.5， 
=3.5， xi2=54．
∴b= 
=0.7
故a=3.5﹣0.7×3.5=1.05，
∴所求线性回归方程为：y=0.7x+1.05
（2）解：将x=10代入回归直线方程，得y=0.7×10+1.05=8.05（小时）．
∴试预测加工10个零件需要8.05个小时
【解析】（1）根据表中所给的数据，做出横标和纵标的平均数，得到样本中心点，求出对应的横标和纵标的积的和，求出横标的平方和，做出系数和a的值，写出线性回归方程．（2）将x=10代入回归直线方程，得y=0.7×10+1.05=8.05．试预测加工10个零件需要8.05个小时，这是一个预报值．
科目：高中数学 来源： 题型：
【题目】已知指数函数y=ax（a＞0，且a≠1）的图象过点（1， 
）．
（I）求函数y=f（x）的解析式；
II）若不等式满足f（2x+1）＞1，求x的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知m、n、s、t∈R* ， m+n=3， 
其中m、n是常数且m＜n，若s+t的最小值 是 
，满足条件的点（m，n）是椭圆 
一弦的中点，则此弦所在的直线方程为（ ）
A.x﹣2y+3=0
B.4x﹣2y﹣3=0
C.x+y﹣3=0
D.2x+y﹣4=0
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列各对直线不互相垂直的是( )
A.l1的倾斜角为120°，l2过点P(1，0)，Q(4， 
)
B.l1的斜率为- 
，l2过点P(1，1)，Q 
C.l1的倾斜角为30°，l2过点P(3， )，Q(4，2 )
D.l1过点M(1，0)，N(4，-5)，l2过点P(-6，0)，Q(-1，3)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，一个矩形花园里需要铺两条笔直的小路，已知矩形花园长AD=5m，宽AB=3m，其中一条小路定为AC，另一条小路过点D，问如何在BC上找到一点M，使得两条小路AC与DM相互垂直？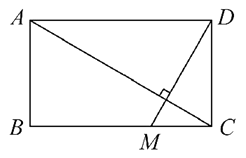
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若抛物线的顶点是双曲线x2﹣y2=1的中心，焦点是双曲线的右顶点
（1）求抛物线的标准方程；
（2）若直线l过点C（2，1）交抛物线于M，N两点，是否存在直线l，使得C恰为弦MN的中点？若存在，求出直线l方程；若不存在，请说明理由．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
