
分析 (1)由椭圆中,e=$\frac{\sqrt{3}}{2}$,焦距为2$\sqrt{3}$,列出方程组,求出a,b,由此能求出椭圆E的方程.
(2)当AB为长轴(或短轴)时,依题意C是椭圆的上下顶点(或左右顶点)时,S△ABC=2.当直线AB的斜率不为0时,设其斜率为k,直线AB的方程为y=kx,联立方程组$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+{y}^{2}=1}\\{y=kx}\end{array}\right.$,得|OA|2=$\frac{4(1+{k}^{2})}{1+4{k}^{2}}$,直线直线OC的方程为y=-$\frac{1}{k}x$,由$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+{y}^{2}=1}\\{y=-\frac{1}{k}x}\end{array}\right.$,得|OC|2=$\frac{4(1+{k}^{2})}{{k}^{2}+4}$.从而求出${S}_{△ABC}≥\frac{8}{5}$,由此能求出△ABC面积的最小值为$\frac{8}{5}$,此时直线直线AB的方程为y=x或y=-x.
解答 解:(1)∵椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,(a>b>0)的e=$\frac{\sqrt{3}}{2}$,焦距为2$\sqrt{3}$,
∴$\left\{\begin{array}{l}{e=\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{2c=2\sqrt{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=2,b=1,
∴椭圆E的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$.
(2)当AB为长轴(或短轴)时,依题意C是椭圆的上下顶点(或左右顶点),
此时S△ABC=$\frac{1}{2}×$|OC|×|AB|=2.
当直线AB的斜率不为0时,设其斜率为k,直线AB的方程为y=kx,
联立方程组$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+{y}^{2}=1}\\{y=kx}\end{array}\right.$,得${{x}_{A}}^{2}$=$\frac{4}{1+4{k}^{2}}$,${{y}_{A}}^{2}=\frac{4{k}^{2}}{1+4{k}^{2}}$,
∴|OA|2=${{x}_{A}}^{2}+{{y}_{A}}^{2}$=$\frac{4(1+{k}^{2})}{1+4{k}^{2}}$,
由|AC|=|CB|知,△ABC为等股三角形,O为AB的中点,OC⊥AB,
∴直线直线OC的方程为y=-$\frac{1}{k}x$,
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+{y}^{2}=1}\\{y=-\frac{1}{k}x}\end{array}\right.$,解得${{x}_{{\;}_{C}}}^{2}$=$\frac{4{k}^{2}}{{k}^{2}+4}$,${{y}_{C}}^{2}$=$\frac{4(1+{k}^{2})}{{k}^{2}+4}$,|OC|2=$\frac{4(1+{k}^{2})}{{k}^{2}+4}$.
S△ABC=2S△OAC=|OA|×|OC|=$\sqrt{\frac{4(1+{k}^{2})}{1+4{k}^{2}}}×\sqrt{\frac{4(1+{k}^{2})}{{k}^{2}+4}}$=$\frac{4(1+{k}^{2})}{\sqrt{(1+4{k}^{2})({k}^{2}+4)}}$.
∵$\sqrt{(1+4{k}^{2})({k}^{2}+4)}$≤$\frac{(1+4{k}^{2})+({k}^{2}+4)}{2}$=$\frac{5({k}^{2}+1)}{2}$,
∴${S}_{△ABC}≥\frac{8}{5}$,
当且仅当1+4k2=k2+4,即k=±1时,等号成立,
此时△ABC面积的最小值是$\frac{8}{5}$,
∵2>$\frac{8}{5}$,∴△ABC面积的最小值为$\frac{8}{5}$,
此时直线直线AB的方程为y=x或y=-x.
点评 本题考查椭圆方程的求法,考查直线方程的求法,是中档题,解题时要认真审题,注意椭圆、直线方程、三角形面积等知识点的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
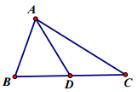 已知△ABC中,点D为BC中点,AB=2,AC=4.
已知△ABC中,点D为BC中点,AB=2,AC=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
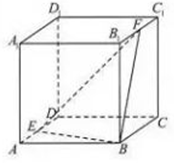 如图,已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱AD,B1C1上的动点,设AE=x,B1F=y,若棱DD1与平面BEF有公共点,则x+y的取值范围是( )
如图,已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱AD,B1C1上的动点,设AE=x,B1F=y,若棱DD1与平面BEF有公共点,则x+y的取值范围是( )| A. | [0,1] | B. | [$\frac{1}{2}$,$\frac{3}{2}$] | C. | [1,2] | D. | [$\frac{3}{2}$,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com