
甲乙两人拿两颗骰子做投掷游戏,规则如下:若掷出的点数之和为3的倍数,原掷骰子的人再继续掷,否则,由对方接着掷。第一次由甲开始掷。
(1)分别求第二次、第三次由甲掷的概率;
(2)求前4次抛掷中甲恰好掷两次的概率.
(1)第二次由甲投的概率为: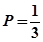 ,第三次由甲投的概率为:
,第三次由甲投的概率为: ;(2)
;(2)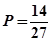
解析试题分析:(1)两颗骰子包含的基本事件共有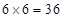 种.
种.
将点数和为3的倍数所有结果一一列出: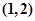 ,
,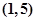 ,
,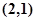 ,
,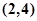 ,
,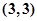 ,
, ,
,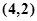 ,
,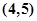 ,
,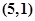 ,
,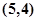 ,
,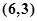 ,
,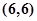 共12种.由此得两骰子点数之和为3的倍数概率为:
共12种.由此得两骰子点数之和为3的倍数概率为: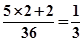
由于第一次由甲掷,所以第二次由甲投,则说明第一次甲掷的结果为点数和为3的倍数.
第三次由甲投,则有两种可能,一种是第一、二次都是3的倍数,一种是第一、二次都不是3 的倍数,将这两个事件的概率相加即得第三次由甲投的概率.
(2)求前4次抛掷中甲恰好掷两次共有以下三种结果:甲甲乙乙,甲乙甲乙,甲乙乙甲.在求概率时,只考虑到第三次,因为第三次确定了,第四次由谁投也就确定了.
试题解析:(1)投两颗骰子包含的基本事件为: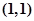 ,
,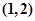 ,
,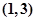 ,
,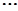 ,
,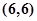 共36.
共36.
点数和为3的倍数有: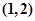 ,
,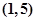 ,
,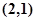 ,
,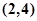 ,
,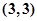 ,
, ,
,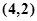 ,
,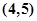 ,
,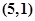 ,
,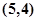 ,
,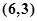 ,
,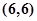 共12种
共12种
两骰子点数之和为3的倍数概率为: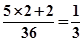 2分
2分
第二次由甲投的概率为: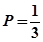
第三次由甲投的概率为: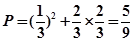 6分
6分
(2)求前4次抛掷中甲恰好掷两次的概率为
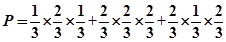
∴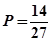 12分
12分
考点:古典概型.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:解答题
袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球n个,已知从袋子中随机抽取1个小球,取到标号为2的小球的概率是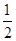 .
.
(1)求n的值;
(2)从袋子中不放回地随机抽取2个球,记第一次取出小球标号为a,第二次取出的小球标号为b.①记“a+b=2”为事件A,求事件A的概率;
②在区间[0,2]内任取2个实数x,y,求事件“x2+y2>(a-b)2恒成立”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了参加2013年市级高中篮球比赛,该市的某区决定从四所高中学校选出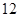 人组成男子篮球队代表所在区参赛,队员来源人数如下表:
人组成男子篮球队代表所在区参赛,队员来源人数如下表:
| 学校 | 学校甲 | 学校乙 | 学校丙 | 学校丁 |
| 人数 | 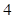 | 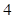 | 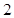 | 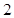 |
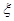 ,求随机变量
,求随机变量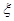 的分布列及数学期望
的分布列及数学期望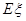 .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
据民生所望,相关部门对所属服务单位进行整治行核查,规定:从甲类3个指标项中随机抽取2项,从乙类2个指标项中随机抽取1项.在所抽查的3个指标项中,3项都优秀的奖励10万元;只有甲类2项优秀的奖励6万元;甲类只有1项优秀、乙类1项优秀的提出警告,有2项或2项以上不优秀的停业运营并罚款8万元.已知某家服务单位甲类3项指标项中有2项优秀,乙类2项指标项中有1项优秀.
求:(1)这家单位受到奖励的概率;
(2)这家单位这次整治性核查中所获金额的均值(奖励为正数,罚款为负数).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校举行演讲比赛,高二(12)班有4名男同学和3名女同学都很想参加这次活动,现从中选一名男同学和一名女同学代表本班参赛,求女同学甲参赛的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为贯彻“激情工作,快乐生物”的理念,某单位在工作之余举行趣味知识有奖竞赛,比赛分初赛和决赛两部分,为了增加节目的趣味性,初赛采用选手选—题答—题的方式进行,每位选手最多有5次选答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰,已知选手甲答题的正确率为 .
.
(1)求选手甲答题次数不超过4次可进入决赛的概率;
(2)设选手甲在初赛中答题的个数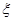 ,试写出
,试写出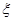 的分布列,并求
的分布列,并求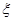 的数学期望。
的数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
小波以游戏方式决定:是去打球、唱歌还是去下棋.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若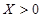 就去打球;若
就去打球;若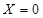 就去唱歌;若
就去唱歌;若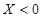 就去下棋.
就去下棋.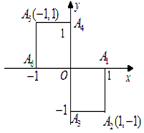
(Ⅰ)分别求小波去下棋的概率和不去唱歌的概率.
(Ⅱ)写出数量积X的所有可能取值,并求X分布列与数学期望
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校为了使运动员顺利参加运动会,招募了8名男志愿者和12名女志愿者,这20名志愿者的身高如下茎叶图(单位:cm):若身高在180cm以上(包括180cm)定义为“高个子”,身高在180cm以下(不包括180cm)定义为“非高个子”,且只有“女高个子”才能担任“礼仪小姐”.
| 男 | | 女 | ||||||
| | | 8 | 16 | 5 | 8 | 9 | | |
| 8 | 7 | 6 | 17 | 2 | 3 | 5 | 5 | 6 |
| 7 | 4 | 2 | 18 | 0 | 1 | 2 | | |
| | | 1 | 19 | 0 | | | | |
 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出 的分布列,并求
的分布列,并求 的数学期望.
的数学期望.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个袋子中装有6个红球和4个白球,假设每一个球被摸到的可能性是相等的.
(Ⅰ)从袋子中摸出3个球,求摸出的球为2个红球和1个白球的概率;
(Ⅱ)从袋子中摸出两个球,其中白球的个数为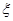 ,求
,求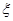 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com