
如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=4,点D是AB的中点, (I)求证:(I)AC⊥BC1;
(II)求证:AC 1//平面CDB1;
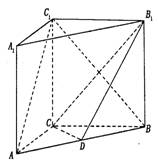
解法一:(I)直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4AB=5,
∴ AC⊥BC,且BC1在平面ABC内的射影为BC,∴ AC⊥BC1;
(II)设CB1与C1B的交点为E,连结DE,∵ D是AB的中点,E是BC1的中点,∴ DE//AC1,∵ DE![]() 平面CDB1,AC1
平面CDB1,AC1![]() 平面CDB1,∴ AC1//平面CDB1;
平面CDB1,∴ AC1//平面CDB1;
解法二:∵直三棱柱ABC-A1B1C1底面三边长AC=3,BC=4,AB=5,∴AC、BC、C1C两两垂直,如图,以C为坐标原点,直线CA、CB、C1C分别为x轴、y轴、z轴,建立空间直角坐标系,则C(0,0,0),A(3,0,0),C1(0,0,4),B(0,4,0),B1(0,4,4),D(![]() ,2,0)
,2,0)
(1)∵![]() =(-3,0,0),
=(-3,0,0),![]() =(0,-4,0),∴
=(0,-4,0),∴![]() ??
??![]() =0,∴AC⊥BC1.
=0,∴AC⊥BC1.
(2)设CB1与C1B的交战为E,则E(0,2,2).∵![]() =(-
=(-![]() ,0,2),
,0,2),![]() =(-3,0,4),∴
=(-3,0,4),∴![]() ,∴DE∥AC1.
,∴DE∥AC1.
(1)证明线线垂直方法有两类:一是通过三垂线定理或逆定理证明,二是通过线面垂直来证明线线垂直;(2)证明线面平行也有两类:一是通过线线平行得到线面平行,二是通过面面平行得到线面平行.
点评:平行问题的转化:
面面平行![]() 线面平行
线面平行![]() 线线平行;
线线平行;
![]()
 主要依据是有关定义及判定定理和性质定理.?
主要依据是有关定义及判定定理和性质定理.?


科目:高中数学 来源: 题型:
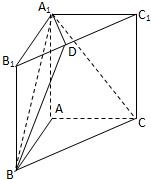 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=a,AC=2,AA1=1,点D在棱B1C1上且B1D:DC1=1:3
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=a,AC=2,AA1=1,点D在棱B1C1上且B1D:DC1=1:3查看答案和解析>>
科目:高中数学 来源: 题型:
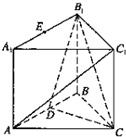 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,D是AB的中点.
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,AB=BC=AA1=2,D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
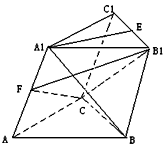
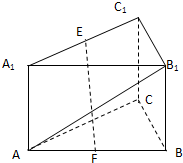 如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=a,E是A1C1的中点,F是AB中点.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=CC1=a,E是A1C1的中点,F是AB中点.查看答案和解析>>
科目:高中数学 来源: 题型:
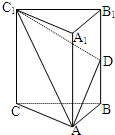 如图,在直三棱柱ABC-A1B1C1中,A1A=AC=
如图,在直三棱柱ABC-A1B1C1中,A1A=AC=| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com