
【题目】在平面直角坐标系中,A、B分别为椭圆![]() 的上、下顶点,若动直线l过点
的上、下顶点,若动直线l过点![]() ,且与椭圆
,且与椭圆![]() 相交于C、D两个不同点(直线l与y轴不重合,且C、D两点在y轴右侧,C在D的上方),直线AD与BC相交于点Q.
相交于C、D两个不同点(直线l与y轴不重合,且C、D两点在y轴右侧,C在D的上方),直线AD与BC相交于点Q.
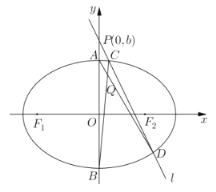
(1)设![]() 的两焦点为
的两焦点为![]() 、
、![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,且
,且![]() ,求点Q的横坐标;
,求点Q的横坐标;
(3)是否存在这样的点P,使得点Q的纵坐标恒为![]() ?若存在,求出点P的坐标,若不存在,请说明理由.
?若存在,求出点P的坐标,若不存在,请说明理由.
【答案】(1)![]() (2)
(2)![]() ;(3)
;(3)![]()
【解析】
(1)由椭圆方程易知∠OAF2=45°,结合对称性可得∠F1AF2=90°;
(2)设C(x1,y1),D(x2,y2),根据已知条件可求得直线BC的方程为y=2x﹣1,直线AD的方程为y=﹣x+1,联立两直线方程即可得到点Q的横坐标;
(3)设直线l的方程为y=kx+b(k<0,b>1),与椭圆方程联立,可得![]() ,直线BC的方程为
,直线BC的方程为![]() ,直线AD的方程为
,直线AD的方程为![]() ,进而得到点Q的纵坐标,由此建立方程化简即可得出结论.
,进而得到点Q的纵坐标,由此建立方程化简即可得出结论.
解:(1)由椭圆Γ的方程知,F1(﹣1,0),F2(1,0),A(0,1),
则∠OAF2=45°,
∴∠F1AF2=90°;
(2)若b=3,设C、D的两点坐标为C(x1,y1),D(x2,y2),
∵![]() ,
,
∴![]() ,即
,即![]() ,
,
而C(x1,y1),D(x2,y2)均在![]() 上,
上,
代入得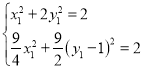 ,解得
,解得![]() ,
,
∴![]() ,分别代入Γ解得,
,分别代入Γ解得,![]() ,
,
∴直线BC的方程为y=2x﹣1,直线AD的方程为y=﹣x+1,
联立![]() ,解得
,解得![]() ,
,
∴Q点的横坐标为![]() ;
;
(3)假设存在这样的点P,设直线l的方程为y=kx+b(k<0,b>1),
点C,D的坐标为C(x1,y1),D(x2,y2),
联立![]() ,得(2k2+1)x2+4kbx+2b2﹣2=0,
,得(2k2+1)x2+4kbx+2b2﹣2=0,
由△=16k2b2﹣8(2k2+1)(b2﹣1)>0,得![]() ,
,
由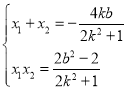 ,可得
,可得![]() ,
,
直线BC的方程为![]() ,直线AD的方程为
,直线AD的方程为![]() ,
,
而x1y2=kx1x2+bx1,x2y1=kx1x2+bx2,联立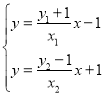 ,
,
得![]()
=![]() ,
,
则b=3>1,因此,存在点P(0,3),使得点Q的纵坐标恒为![]() .
.


科目:高中数学 来源: 题型:
【题目】年前某市质监部门根据质量管理考核指标对本地的500家食品生产企业进行考核,然后通过随机抽样抽取其中的50家,统计其考核成绩(单位:分),并制成如下频率分布直方图.
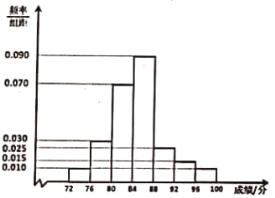
(1)求这50家食品生产企业考核成绩的平均数![]() (同一组中的数据用该组区间的中点值为代表)及中位数a(精确到0.01)
(同一组中的数据用该组区间的中点值为代表)及中位数a(精确到0.01)
(2)该市质监部门打算举办食品生产企业质量交流会,并从这50家食品生产企业中随机抽取4家考核成绩不低于88分的企业发言,记抽到的企业中考核成绩在![]() 的企业数为X,求X的分布列与数学期望
的企业数为X,求X的分布列与数学期望
(3)若该市食品生产企业的考核成绩X服从正态分布![]() 其中
其中![]() 近似为50家食品生产企业考核成绩的平均数
近似为50家食品生产企业考核成绩的平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,经计算得
,经计算得![]() ,利用该正态分布,估计该市500家食品生产企业质量管理考核成绩高于90.06分的有多少家?(结果保留整数).
,利用该正态分布,估计该市500家食品生产企业质量管理考核成绩高于90.06分的有多少家?(结果保留整数).
附参考数据与公式:
![]()
![]()
则![]() ,
,![]() .
.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 中,
中,![]() 与
与![]() 均为等腰直角三角形,且
均为等腰直角三角形,且![]() ,
,![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() 平面
平面![]() .
.
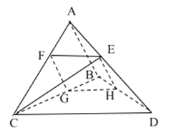
(1)求证:![]() ;
;
(2)过![]() 作一平面分别交
作一平面分别交![]() ,
, ![]() ,
, ![]() 于
于![]() ,
,![]() ,
,![]() ,若四边形
,若四边形![]() 为平行四边形,求多面体
为平行四边形,求多面体![]() 的表面积.
的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中某班共有40个学生,将学生的身高分成4组:平频率/组距![]() ,
,![]() ,
,![]() ,
,![]() 进行统计,作成如图所示的频率分布直方图.
进行统计,作成如图所示的频率分布直方图.
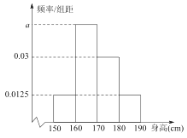
(1)求频率分布直方图中![]() 的值和身高在
的值和身高在![]() 内的人数;
内的人数;
(2)求这40个学生平均身高的估计值(同一组中的数据用该组区间的中点值为代表)(精确到0.01).
查看答案和解析>>
科目:高中数学 来源: 题型:
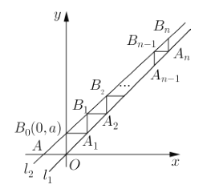
【题目】已知直线![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 与x轴交于点A,与y轴交于点
与x轴交于点A,与y轴交于点![]() ,过
,过![]() 作x 轴的平行线,交
作x 轴的平行线,交![]() 于点
于点![]() ,过
,过![]() 作y轴的平行线,交
作y轴的平行线,交![]() 于点
于点![]() ,再过
,再过![]() 作x轴的平行线交
作x轴的平行线交![]() 于点
于点![]() ,…,这样依次得线段
,…,这样依次得线段![]() 、
、![]() 、
、![]() 、
、![]() 、…、
、…、![]() 、
、![]() ,记
,记![]() 为点
为点![]() 的横坐标,则
的横坐标,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 处的切线方程
处的切线方程![]() ,求实数a,b的值;
,求实数a,b的值;
(2)若函数![]() 在
在![]() 和
和![]() 两处得极值,求实数a的取值范围;
两处得极值,求实数a的取值范围;
(3)在(2)的条件下,若![]() .求实数a的取值范围.
.求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是椭圆C:
是椭圆C: ![]() 上一点,点P到椭圆C的两个焦点的距离之和为
上一点,点P到椭圆C的两个焦点的距离之和为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设A,B是椭圆C上异于点P的两点,直线PA与直线![]() 交于点M,
交于点M,
是否存在点A,使得![]() ?若存在,求出点A的坐标;若不存在,请说明理由.
?若存在,求出点A的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 的参数方程为
的参数方程为![]() (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程以及曲线C的参数方程;
的普通方程以及曲线C的参数方程;
(2)过曲线C上任意一点M作与直线![]() 的夹角为
的夹角为![]() 的直线,交
的直线,交![]() 于点N,求
于点N,求![]() 的最小值
的最小值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 中,三个内角
中,三个内角![]() ,
,![]() ,
,![]() 所对的边分别是
所对的边分别是![]() ,
,![]() ,
,![]() .
.
(1)证明:![]() ;
;
(2)在①![]() ,②
,②![]() ,③
,③![]() 这三个条件中任选一个补充在下面问题中,并解答
这三个条件中任选一个补充在下面问题中,并解答
若![]() ,
,![]() ,________,求
,________,求![]() 的周长.
的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com