
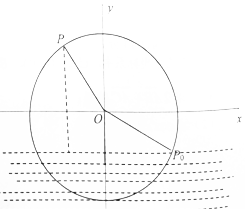
 一半径为4米的水轮如图所示,水轮圆心O距离水面2米,已知水轮每60秒逆时针转动5圈,如果当水轮上点P从水中浮现时(图象P0点)开始计算时间,且点P距离水面的高度f(t)(米)与时间t(秒)满足函数:f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).
一半径为4米的水轮如图所示,水轮圆心O距离水面2米,已知水轮每60秒逆时针转动5圈,如果当水轮上点P从水中浮现时(图象P0点)开始计算时间,且点P距离水面的高度f(t)(米)与时间t(秒)满足函数:f(t)=Asin(ω+φ)+B(A>0,ω>0,|φ|<$\frac{π}{2}$).分析 (1)先根据z的最大和最小值求得A和B,利用周期求得ω,当x=0时,z=0,进而求得φ的值,则函数的表达式可得;
(2)令f(t)=4sin($\frac{π}{6}t-\frac{π}{6}$)+2=6,)⇒sin($\frac{π}{6}t-\frac{π}{6}$)=1,$\frac{π}{6}t-\frac{π}{6}$=$\frac{5π}{2}$解得t.
解答 解:(1)依题意可知z的最大值为6,最小为-2,∴$\left\{\begin{array}{l}{A+B=6}\\{-A+B=-2}\end{array}\right.∴\left\{\begin{array}{l}{A=4}\\{B=2}\end{array}\right.$,
$\frac{5×2π}{60}\frac{π}{6}$,∴f(t)=4sin($\frac{π}{6}t+$φ)+2,当t=0时,f(t)=0,得sinφ=-$\frac{1}{2}$,φ=-$\frac{π}{6}$,
故所求的函数关系式为f(t)=4sin($\frac{π}{6}t-\frac{π}{6}$)+2,
(2)令f(t)=4sin($\frac{π}{6}t-\frac{π}{6}$)+2=6,)⇒sin($\frac{π}{6}t-\frac{π}{6}$)=1,
$\frac{π}{6}t-\frac{π}{6}$=$\frac{5π}{2}$
得t=16,
故点P第二次到达最高点大约需要16s.
点评 本题主要考查了在实际问题中建立三角函数模型的问题.考查了运用三角函数的最值,周期等问题确定函数的解析式,属于中档题.


科目:高中数学 来源: 题型:解答题
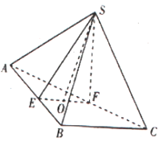 如图,三棱锥S-ABC,E,F分别在线段AB,AC上,EF∥BC,△ABC,△SEF均是等边三角形,且平面SEF⊥平面ABC,若BC=4,EF=a,O为EF的中点.
如图,三棱锥S-ABC,E,F分别在线段AB,AC上,EF∥BC,△ABC,△SEF均是等边三角形,且平面SEF⊥平面ABC,若BC=4,EF=a,O为EF的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6、 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{10}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com