
分析 由两角差的正弦公式化简$sinA-cosA=\frac{{\sqrt{2}}}{2}$,由A的范围和特殊角的三角函数值求出角A的度数;利用两角和的正弦公式求出sianA,代入三角形的面积公式求出△ABC的面积.
解答 解:由题意得,$sinA-cosA=\frac{{\sqrt{2}}}{2}$,
∴$\sqrt{2}sin(A-\frac{π}{4})=\frac{\sqrt{2}}{2}$,则$sin(A-\frac{π}{4})=\frac{1}{2}$,
∵0<A<π,∴$A-\frac{π}{4}=\frac{π}{6}$,则A=$\frac{5π}{12}$,
∴sin$\frac{5π}{12}$=sin($\frac{π}{4}+\frac{π}{6}$)=$\frac{\sqrt{2}}{2}(\frac{1}{2}+\frac{\sqrt{3}}{2})$=$\frac{\sqrt{6}+\sqrt{2}}{4}$,
∵AC=2,AB=4,
∴△ABC的面积S=$\frac{1}{2}•AC•ABsinA$=$\frac{1}{2}×2×4×\frac{\sqrt{6}+\sqrt{2}}{4}$
=$\sqrt{6}+\sqrt{2}$,
综上,角A的度数是$\frac{5π}{12}$;△ABC的面积是$\sqrt{6}+\sqrt{2}$.
点评 本题考查两角和与差的正弦公式,三角形的面积公式,注意内角的范围,考查化简、变形能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
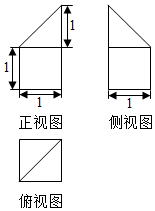
| A. | $\frac{7}{6}$cm3 | B. | $\frac{4}{3}$cm3 | C. | $\frac{3}{2}$cm3 | D. | 2cm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
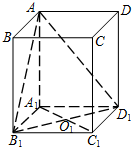 已知ABCD-A1B1C1D1是底面边长为1的正四棱柱,O1是A1C1和B1D1的交点.
已知ABCD-A1B1C1D1是底面边长为1的正四棱柱,O1是A1C1和B1D1的交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{3π}{4}$] | B. | [0,$\frac{π}{4}$] | C. | [0,$\frac{π}{4}$]∪($\frac{π}{2}$,$\frac{3π}{4}$] | D. | [$\frac{π}{4}$,$\frac{π}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①简单随机抽样,②系统抽样,③分层抽样 | |
| B. | ①分层抽样,②系统抽样,③简单随机抽样 | |
| C. | ①系统抽样,②简单随机抽样,③分层抽样 | |
| D. | ①简单随机抽样,②分层抽样,③系统抽样 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | -$\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
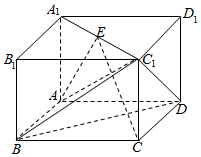 在长方体ABCD-A1B1C1D1中,E是A1C1与B1D1的交点,AB=BC=$\sqrt{2}$,AA1=1.
在长方体ABCD-A1B1C1D1中,E是A1C1与B1D1的交点,AB=BC=$\sqrt{2}$,AA1=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com