
分析 由2|AB1|=3|B1D|,得:$\frac{{|A{B_1}|}}{|AD|}=\frac{3}{5}$,根据三角形相似得:$\frac{a}{{a-{x_0}}}=\frac{3}{5}=\frac{b}{y_0}$,则${x_0}=-\frac{2}{3}a,{y_0}=\frac{5}{3}b$,代入即可求得e的值.
解答 解:如图所示,设D(x0,y0),由2|AB1|=3|B1D|,得:$\frac{{|A{B_1}|}}{|AD|}=\frac{3}{5}$,
根据三角形相似得:$\frac{a}{{a-{x_0}}}=\frac{3}{5}=\frac{b}{y_0}$,求得:${x_0}=-\frac{2}{3}a,{y_0}=\frac{5}{3}b$,
又直线B2F1的方程为$\frac{x}{-c}+\frac{y}{-b}=1$
将点$D(-\frac{2}{3}a,\frac{5}{3}b)$代入,得:$\frac{{-\frac{2}{3}a}}{-c}+\frac{{\frac{5}{3}b}}{-b}=1,\frac{2}{3e}=1+\frac{5}{3}=\frac{8}{3}$,
∴$e=\frac{2}{3}×\frac{3}{8}=\frac{1}{4}$.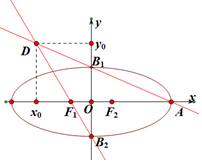
故答案为:$\frac{1}{4}$.
点评 本题考查椭圆的离心率,考查三角形的相似的性质,考查数形结合思想的应用,属于中档题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{7}{25}$ | B. | $\frac{7}{25}$ | C. | 一$\frac{16}{25}$ | D. | $\frac{16}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
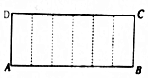 已知矩形ABCD的周长为18,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为( )
已知矩形ABCD的周长为18,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为( )| A. | 13π | B. | 12π | C. | 11π | D. | 10π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-e) | B. | (-∞,-$\frac{{e}^{2}}{4}$) | C. | (-∞,-$\frac{{e}^{3}}{9}$) | D. | (-∞,-$\frac{{e}^{4}}{16}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com