
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是直角梯形,且
是直角梯形,且![]()
![]() ,
,![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
科目:高中数学 来源: 题型:
【题目】如图所示, ![]() 是边长为3的正方形,
是边长为3的正方形, ![]() 平面
平面![]() 与平面
与平面![]() 所成角为
所成角为![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)设点![]() 是线段
是线段![]() 上一个动点,试确定点
上一个动点,试确定点![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ,并证明你的结论.
,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表表示的是某款车的车速与刹车距离的关系,试分别就![]() ,
,![]() ,
,![]() 三种函数关系建立数学模型,并探讨最佳模拟,根据最佳模拟求车速为120km/h时的刹车距离.
三种函数关系建立数学模型,并探讨最佳模拟,根据最佳模拟求车速为120km/h时的刹车距离.
车速/(km/h) | 10 | 15 | 30 | 40 | 50 |
刹车距离/m | 4 | 7 | 12 | 18 | 25 |
车速/((km/h) | 60 | 70 | 80 | 90 | 100 |
刹车距离/m | 34 | 43 | 54 | 66 | 80 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接2022年北京冬奥会,推广滑雪运动,某滑雪场开展滑雪促销活动.该滑雪场的收费标准是:滑雪时间不超过1小时免费,超过1小时的部分每小时收费标准为40元(不足1小时的部分按1小时计算).有甲、乙两人相互独立地来该滑雪场运动,设甲、乙不超过1小时离开的概率分别为![]() ,
,![]() ;1小时以上且不超过2小时离开的概率分别为
;1小时以上且不超过2小时离开的概率分别为![]() ,
,![]() ;两人滑雪时间都不会超过3小时.
;两人滑雪时间都不会超过3小时.
(1)求甲、乙两人所付滑雪费用相同的概率;
(2)设甲、乙两人所付的滑雪费用之和为随机变量ξ,求ξ的分布列与数学期望E(ξ).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (常数
(常数![]() )满足
)满足![]() .
.
(1)求![]() 的值,并对常数
的值,并对常数![]() 的不同取值讨论函数
的不同取值讨论函数![]() 奇偶性;
奇偶性;
(2)若![]() 在区间
在区间![]() 上单调递减,求
上单调递减,求![]() 的最小值.
的最小值.
(3)若方程![]() 在
在![]() 有解,求
有解,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于回归分析与独立性检验的说法正确的是()
A.回归分析和独立性检验没有什么区别;
B.回归分析是对两个变量准确关系的分析,而独立性检验是分析两个变量之间的不确定性关系;
C.独立性检验可以![]() 确定两个变量之间是否具有某种关系.
确定两个变量之间是否具有某种关系.
D.回归分析研究两个变量之间的相关关系,独立性检验是对两个变量是否具有某种关系的一种检验;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县共有90间农村淘宝服务站,随机抽取5间,统计元旦期间的网购金额(单位:万元)的茎叶图如图所示,其中茎为十位数,叶为个位数.
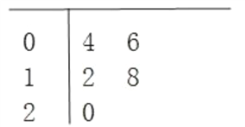
(1)根据茎叶图计算样本均值;
(2)若网购金额(单位:万元)不小于18的服务站定义为优秀服务站,其余为非优秀服务站.根据茎叶图推断90间服务站中有几间优秀服务站?
(3)从随机抽取的5间服务站中再任取2间作网购商品的调查,求恰有1间是优秀服务站的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在贯彻中共中央国务院关于精准扶贫政策的过程中,某单位定点帮扶甲、乙两个村各50户贫困户.为了做到精准帮扶,工作组对这100户村民的年收入情况、劳动能力情况、子女受教育情况、危旧房情况、患病情况等进行调查,并把调查结果转化为各户的贫困指标![]() 和
和![]() ,制成下图,其中“
,制成下图,其中“![]() ”表示甲村贫困户,“
”表示甲村贫困户,“![]() ”表示乙村贫困户.若
”表示乙村贫困户.若![]() ,则认定该户为“绝对贫困户”,若
,则认定该户为“绝对贫困户”,若![]() ,则认定该户为“相对贫困户”,若
,则认定该户为“相对贫困户”,若![]() ,则认定该户为“低收入户”;若
,则认定该户为“低收入户”;若![]() ,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
,则认定该户为“今年能脱贫户”,否则为“今年不能脱贫户”.
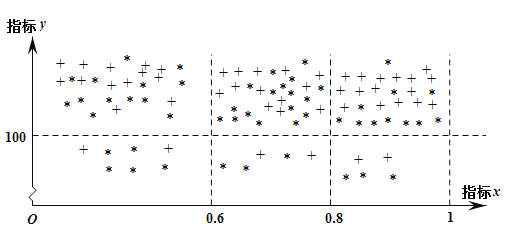
(1)从乙村的50户中随机选出一户,求该户为“绝对贫困户”的概率;
(2)从甲村所有“今年不能脱贫的非绝对贫困户”中任选2户,求选出的2户均为“低收入户”的概率;
(3)试比较这100户中,甲、乙两村指标![]() 的方差的大小(只需写出结论).
的方差的大小(只需写出结论).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com