
【题目】已知函数![]() (
(![]() ,
, ![]() =2.718………),
=2.718………),
(I) 当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(II)当![]() 时,不等式
时,不等式![]() 对任意
对任意![]() 恒成立,
恒成立,
求实数![]() 的最大值.
的最大值.
【答案】(1)函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ;
;
(2)符合题意的实数![]() 的最大值为
的最大值为![]() .
.
【解析】试题分析:(1)求函数单调区间,即求导研究导函数的正负,导函数大于零求增区间,导函数小于零求减区间;(2)这是不等式恒成立求参的问题,转化为![]() ,
, ![]() 对任意
对任意![]() 恒成立,再求导研究函数的单调性,求最值即可.
恒成立,再求导研究函数的单调性,求最值即可.
(1)![]()
由![]() 可知,
可知, ![]()
令![]() 得
得 ![]() 或
或![]()
令![]() 得
得 ![]()
即 此时函数![]() 的单调递增区间为
的单调递增区间为![]() 和
和![]() ,单调递减区间为
,单调递减区间为![]() ;
;
(2)当![]() 时,不等式
时,不等式![]() 即
即 ![]()
令![]() ,
, ![]() 对任意
对任意![]() 恒成立
恒成立
又 ![]()
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上递增,且最小值为
上递增,且最小值为![]()
(i)当![]() ,即
,即![]() 时,
时, ![]() 对任意
对任意![]() 恒成立
恒成立
![]()
![]() 在
在![]() 上递增,
上递增, ![]() 当
当![]() 时,
时, ![]() 满足题意; (ii)当
满足题意; (ii)当![]() ,即
,即![]() 时,
时,
由上可得存在唯一的实数![]() ,使得
,使得![]() ,可得当
,可得当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 上递减,此时
上递减,此时![]() 不符合题意; 综上得,当
不符合题意; 综上得,当时,满足题意,即符合题意的实数
![]() 的最大值为
的最大值为![]() .
.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】某出租车公司响应国家节能减排的号召,已陆续购买了140辆纯电动汽车作为运营车辆,目前我国主流纯电动汽车按续航里程数![]() .(单位:公里)分为3类,即
.(单位:公里)分为3类,即![]() 类:
类:![]() ,
,![]() 类:
类:![]() ,
, ![]() 类:
类:![]() ,该公司对这140辆车的行驶总里程进行统计,结果如下表:
,该公司对这140辆车的行驶总里程进行统计,结果如下表:
类型 |
|
|
|
已行驶总里程不超过10万公里的车辆数 | 10 | 40 | 30 |
已行驶总里程超过10万公里的车辆数 | 20 | 20 | 20 |
(1)从这140辆汽车中任取一辆,求该车行驶总里程超过10万公里的概率;
(2)公司为了了解这些车的工作状况,决定抽取了14辆车进行车况分析,按表中描述的六种情况进行分层抽样,设从![]() 类车中抽取了
类车中抽取了![]() 辆车.
辆车.
①求![]() 的值;
的值;
②如果从这![]() 辆车中随机选取两辆车,求恰有一辆车行驶总里程超过10万公里的概率.
辆车中随机选取两辆车,求恰有一辆车行驶总里程超过10万公里的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(2cosωx,cos2ωx),
=(2cosωx,cos2ωx), ![]() =(sinωx,1)(其中ω>0),令f(x)=
=(sinωx,1)(其中ω>0),令f(x)= ![]() ,且f(x)的最小正周期为π.
,且f(x)的最小正周期为π.
(1)求 ![]() 的值;
的值;
(2)写出 ![]() 上的单调递增区间.
上的单调递增区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,离心率为
,离心率为![]() ,设直线
,设直线![]() 的斜率是
的斜率是![]() ,且
,且![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆的标准方程.
(Ⅱ)若直线![]() 在
在![]() 轴上的截距是
轴上的截距是![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
(Ⅲ)以![]() 为底作等腰三角形,顶点为
为底作等腰三角形,顶点为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线![]() ,直线
,直线![]() (其中
(其中![]() )与曲线
)与曲线![]() 相交于
相交于![]() 、
、![]() 两点.
两点.
(Ⅰ)若![]() ,试判断曲线
,试判断曲线![]() 的形状.
的形状.
(Ⅱ)若![]() ,以线段
,以线段![]() 、
、![]() 为邻边作平行四边形
为邻边作平行四边形![]() ,其中顶点
,其中顶点![]() 在曲线
在曲线![]() 上,
上, ![]() 为坐标原点,求
为坐标原点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点
的焦点![]() 在直线
在直线![]() 上,且抛物线
上,且抛物线![]() 截直线
截直线![]() 所得的弦
所得的弦![]() 的长为
的长为![]() .
.
(Ⅰ)求抛物线![]() 的方程和
的方程和![]() 的值.
的值.
(Ⅱ)以弦![]() 为底边,以
为底边,以![]() 轴上点
轴上点![]() 为顶点的三角形
为顶点的三角形![]() 面积为
面积为![]() ,求点
,求点![]() 坐标.
坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知公比为负值的等比数列{an}中,a1a5=4,a4=﹣1.
(1)求数列{an}的通项公式;
(2)设bn= ![]() +
+ ![]() +…+
+…+ ![]() ,求数列{an+bn}的前n项和Sn .
,求数列{an+bn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记Sn为正项等比数列{an}的前n项和,若 ![]() ﹣7
﹣7 ![]() ﹣8=0,且正整数m,n满足a1ama2n=2
﹣8=0,且正整数m,n满足a1ama2n=2 ![]() ,则
,则 ![]() +
+ ![]() 的最小值是( )
的最小值是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“新零售”模式的背景下,某大型零售公司咪推广线下分店,计划在![]() 市的
市的![]() 区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记
区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店听其他区的数据作了初步处理后得到下列表格.记![]() 表示在各区开设分店的个数,
表示在各区开设分店的个数, ![]() 表示这个
表示这个![]() 个分店的年收入之和.
个分店的年收入之和.
| 2 | 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 | 6 |
(1)该公司已经过初步判断,可用线性回归模型拟合![]() 与
与![]() 的关系,求
的关系,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)假设该公司在![]() 区获得的总年利润
区获得的总年利润![]() (单位:百万元)与
(单位:百万元)与![]() 之间的关系为
之间的关系为![]() ,请结合(1)中的线性回归方程,估算该公司应在
,请结合(1)中的线性回归方程,估算该公司应在![]() 区开设多少个分时,才能使
区开设多少个分时,才能使![]() 区平均每个分店的年利润最大?
区平均每个分店的年利润最大?
(参考公式: ![]() ,其中
,其中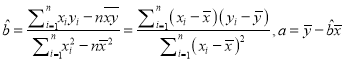 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com