
(2004
江苏,19)制订投资计划时,不仅要考虑可能获得的盈利,而且要考虑可能出现的亏损.某投资人打算投资甲、乙两个项目,根据预测,甲、乙项目可能的最大盈利率分别为100%和50%,可能的最大亏损率分别为30%和10%,投资人计划投资金额不超过10万元,要求确保可能的资金亏损不超过1.8万元,问投资人对甲、乙两个项目各投资多少万元,才能使可能的盈利最大?|
解析:设投资人分别用 x万元、y万元投资甲、乙两个项目,由题意知 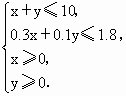 目标函数z=x+0.5y. 目标函数z=x+0.5y.
上述不等式组表示的平面区域如图所示,阴影部分 (含边界)即可行域.作直线 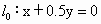 ,并作平行于直线 ,并作平行于直线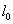 的一组直线x+0.5y=z,z 的一组直线x+0.5y=z,z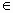 R, R,
与可行域相交,其中有一条直线经过可行域上的 M点,且与直线x+0.5y=0的距离最大,这里M点是直线x+y=10和0.3x+0.1y=1.8的交点.解方程组 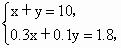 得x=4,y=6, 得x=4,y=6,
此时 z=1×4+0.5×6=7(万元).∵ 7>0,∴当 x=4,y=6时z取得最大值.
答:投资人用 4万元投资甲项目、6万元投资乙项目,才能在确保亏损不超过1.8万元的前提下,使可能的盈利最大. |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com