


科目:高中数学 来源:名师指点学高中课程 数学 高二(下) 题型:044
已知下列四个命题:
①设正三棱锥两侧面所成二面角为 ,则
,则 ;
;
②正四棱锥相邻两侧面所成二面角的平面角必是钝角;
③正四棱锥的底面面积为Q,全面积为P,则侧面与底面所成的二面角的大小为arc cos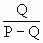 ;
;
④四棱锥P-ABCD中,PA⊥底面ABCD,且ABCD是正方形,则侧面PAB与PBC所成的二面角是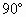 .
.
其中正确命题的题号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
A.60°<θ<180° B.θ<60°
C.θ>90° D.θ>60°或θ<60°
查看答案和解析>>
科目:高中数学 来源:高考数学一轮复习必备(第79课时):第九章 直线、平面、简单几何体-平面所成的角(解析版) 题型:选择题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com