
设函数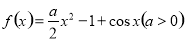 .
.
(1)当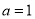 时,求函数
时,求函数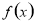 在
在 上的最大值和最小值;
上的最大值和最小值;
(2)若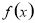 在
在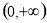 上为增函数,求正数
上为增函数,求正数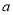 的取值范围.
的取值范围.
(1)最小值为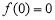 ,最大值为
,最大值为 ;(2)
;(2)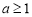 .
.
【解析】
试题分析:(1)当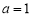 时,
时,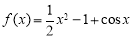 ,其导函数
,其导函数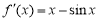 ,易得当
,易得当 时,
时,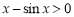 ,即函数
,即函数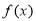 在区间
在区间 上单调递增,又函数
上单调递增,又函数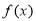 是偶函数,所以函数
是偶函数,所以函数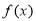 在
在 上单调递减,
上单调递减,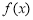 在
在 上的最小值为
上的最小值为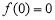 ,最大值为
,最大值为 ;
;
(2)由题得: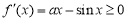 在
在 上恒成立,易证
上恒成立,易证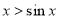 ,若
,若 时,则
时,则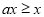 ,所以
,所以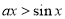 ;若
;若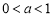 时,易证此时不成立.
时,易证此时不成立.
(1)当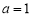 时,
时,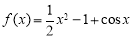 ,
, 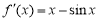 ,
,
令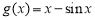 ,则
,则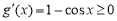 恒成立,
恒成立,
∴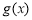 为增函数,
为增函数,
故当 时,
时,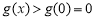
∴当 时,
时,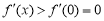 ,∴
,∴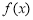 在
在 上为增函数,
上为增函数,
又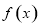 为偶函数,
为偶函数,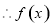 在
在 上为减函数,
上为减函数,
∴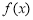 在
在 上的最小值为
上的最小值为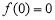 ,最大值为
,最大值为 .
.
(2)由题意,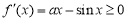 在
在 上恒成立.
上恒成立.
(ⅰ)当 时,对
时,对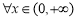 ,恒有
,恒有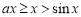 ,此时
,此时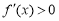 ,函数
,函数 在
在 上为增函数,满足题意;
上为增函数,满足题意;
(ⅱ)当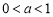 时,令
时,令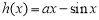 ,
,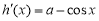 ,由
,由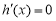 得
得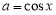 ,
,
一定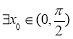 ,使得
,使得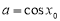 ,且当
,且当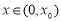 时,
时,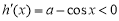 ,
,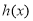 在
在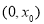 上单调递减,此时
上单调递减,此时 ,即
,即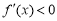 ,所以
,所以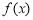 在
在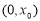 为减函数,这与
为减函数,这与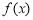 在
在 为增函数矛盾.
为增函数矛盾.
综上所述: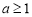 .
.
考点:函数的最值;函数的恒成立问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2013-2014学年安徽省合肥市高三第二次教学质量检测理科数学试卷(解析版) 题型:填空题
合肥市环保总站发布2014年1月11日到1月20日的空气质量指数(AQI),数据如下:153、203、268、166、157、164、268、407、335、119,则这组数据的中位数是________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省“皖西七校”高三年级联合考试理科数学试卷(解析版) 题型:选择题
已知数列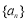 是等差数列,
是等差数列,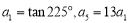 ,设
,设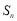 为数列
为数列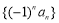 的前
的前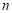 项和,则
项和,则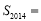 ( )
( )
A.2014 B. C.3021 D.
C.3021 D.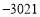
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省“皖西七校”高三年级联合考试文科数学试卷(解析版) 题型:选择题
已知圆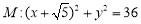 ,定点
,定点 ,点
,点 为圆
为圆 上的动点,点
上的动点,点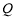 在
在 上,点
上,点 在线段
在线段 上,且满足
上,且满足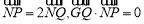 ,则点
,则点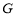 的轨迹方程是( )
的轨迹方程是( )
A. B.
B. C.
C. D.
D.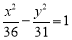
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省“皖西七校”高三年级联合考试文科数学试卷(解析版) 题型:选择题
“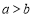 ”是“
”是“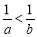 ”的( )
”的( )
A.充分必要条件 B.必要不充分条件
C.充分不必要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2013-2014学年安徽省“江淮十校协作体”四月联考卷理科数学试卷(解析版) 题型:选择题
一排9个座位坐了3个三口之家,若每家人坐在一起,则不同的坐法种是为( )
A.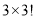 B.
B.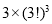 C.
C.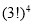 D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年天津市蓟县高三第一次模拟考试理科数学试卷(解析版) 题型:解答题
已知数列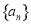 满足:
满足: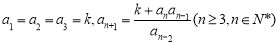 其中
其中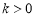 ,数列
,数列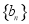 满足:
满足: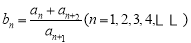
(1)求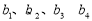 ;
;
(2)求数列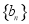 的通项公式;
的通项公式;
(3)是否存在正数k,使得数列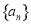 的每一项均为整数,如果不存在,说明理由,如果存在,求出所有的k.
的每一项均为整数,如果不存在,说明理由,如果存在,求出所有的k.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com