
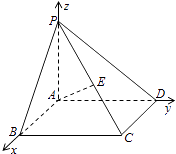
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点,已知AB=2,AD=2 ![]() ,PA=2,求:
,PA=2,求: 
(1)三角形PCD的面积;
(2)异面直线BC与AE所成的角的大小.
【答案】
(1)解:∵PA⊥底面ABCD,CD底面ABCD,
∴CD⊥PA.
∵矩形ABCD中,CD⊥AD,而PA、AD是平面PAD的交线.
∴CD⊥平面PDA,
∵PD平面PDA,∴CD⊥PD,三角形PCD是以D为直角顶点的直角三角形.
∵Rt△PAD中,AD=2 ![]() ,PA=2,
,PA=2,
∴PD= ![]() =2
=2 ![]() .
.
∴三角形PCD的面积S= ![]() ×PD×DC=2
×PD×DC=2 ![]() .
.
(2)解:[解法一]
如图所示,建立空间直角坐标系,可得B(2,0,0),C(2,2 ![]() ,0),E(1,
,0),E(1, ![]() ,1).
,1).
∴ ![]() =(1,
=(1, ![]() ,1),
,1), ![]() =(0,2
=(0,2 ![]() ,0),
,0),
设 ![]() 与
与 ![]() 夹角为θ,则cosθ=
夹角为θ,则cosθ= 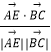 =
= ![]() =
= ![]() ,
,
∴θ= ![]() ,由此可得异面直线BC与AE所成的角的大小为
,由此可得异面直线BC与AE所成的角的大小为 ![]() .
.
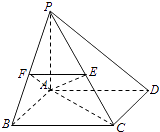
[解法二]
取PB的中点F,连接AF、EF、AC,
∵△PBC中,E、F分别是PC、PB的中点,
∴EF∥BC,∠AEF或其补角就是异面直线BC与AE所成的角.
∵Rt△PAC中,PC= ![]() =4.
=4.
∴AE= ![]() PC=2,
PC=2,
∵在△AEF中,EF= ![]() BC=
BC= ![]() ,AF=
,AF= ![]() PB=
PB= ![]()
∴AF2+EF2=AE2,△AEF是以F为直角顶点的等腰直角三角形,
∴∠AEF= ![]() ,可得异面直线BC与AE所成的角的大小为
,可得异面直线BC与AE所成的角的大小为 ![]() .
.
【解析】(1)可以利用线面垂直的判定与性质,证明出三角形PCD是以D为直角顶点的直角三角形,然后在Rt△PAD中,利用勾股定理得到PD=2 ![]() ,最后得到三角形PCD的面积S;(2)[解法一]建立如图空间直角坐标系,可得B、C、E各点的坐标,从而
,最后得到三角形PCD的面积S;(2)[解法一]建立如图空间直角坐标系,可得B、C、E各点的坐标,从而 ![]() =(1,
=(1, ![]() ,1),
,1), ![]() =(0,2
=(0,2 ![]() ,0),利用空间向量数量积的公式,得到
,0),利用空间向量数量积的公式,得到 ![]() 与
与 ![]() 夹角θ满足:cosθ=
夹角θ满足:cosθ= ![]() ,由此可得异面直线BC与AE所成的角的大小为
,由此可得异面直线BC与AE所成的角的大小为 ![]() ;[解法二]取PB的中点F,连接AF、EF,△PBC中,利用中位线定理,得到EF∥BC,从而∠AEF或其补角就是异面直线BC与AE所成的角,然后可以通过计算证明出:△AEF是以F为直角顶点的等腰直角三角形,所以∠AEF=
;[解法二]取PB的中点F,连接AF、EF,△PBC中,利用中位线定理,得到EF∥BC,从而∠AEF或其补角就是异面直线BC与AE所成的角,然后可以通过计算证明出:△AEF是以F为直角顶点的等腰直角三角形,所以∠AEF= ![]() ,可得异面直线BC与AE所成的角的大小为
,可得异面直线BC与AE所成的角的大小为 ![]() .
.
【考点精析】本题主要考查了异面直线及其所成的角和直线与平面垂直的性质的相关知识点,需要掌握异面直线所成角的求法:1、平移法:在异面直线中的一条直线中选择一特殊点,作另一条的平行线;2、补形法:把空间图形补成熟悉的或完整的几何体,如正方体、平行六面体、长方体等,其目的在于容易发现两条异面直线间的关系;垂直于同一个平面的两条直线平行才能正确解答此题.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
【题目】袋子中有大小、形状完全相同的四个小球,分别写有和、“谐”、“校”“园”四个字,有放回地从中任意摸出一个小球,直到“和”、“谐”两个字都摸到就停止摸球,用随机模拟的方法估计恰好在第三次停止摸球的概率。利用电脑随机产生![]() 到
到![]() 之间取整数值的随机数,分别用
之间取整数值的随机数,分别用![]() ,
,![]() ,
,![]() ,
,![]() 代表“和”、“谐”、“校”、“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下
代表“和”、“谐”、“校”、“园”这四个字,以每三个随机数为一组,表示摸球三次的结果,经随机模拟产生了以下![]() 组随机数:
组随机数:
![]()
由此可以估计,恰好第三次就停止摸球的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计的频率分布直方图如图所示.
(单位:克)中,经统计的频率分布直方图如图所示.

(1)估计这组数据的平均数(同一组中的数据以这组数据所在区间中点的值作代表);
(2)现按分层抽样从质量为[200,250),[250,300)的芒果中随机抽取5个,再从这5个中随机抽取2个,求这2个芒果都来自同一个质量区间的概率;
(3)某经销商来收购芒果,同一组中的数据以这组数据所在区间中点的值作代表,用样本估计总体,该种植园中还未摘下的芒果大约还有10000个,经销商提出以下两种收购方案:
方案①:所有芒果以9元/千克收购;
方案②:对质量低于250克的芒果以2元/个收购,对质量高于或等于250克的芒果以3元/个收购.
通过计算确定种植园选择哪种方案获利更多.
参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设10≤x1<x2<x3<x4≤104 , x5=105 , 随机变量ξ1取值x1、x2、x3、x4、x5的概率均为0.2,随机变量ξ2取值 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 、
、 ![]() 的概率也均为0.2,若记Dξ1、Dξ2分别为ξ1、ξ2的方差,则( )
的概率也均为0.2,若记Dξ1、Dξ2分别为ξ1、ξ2的方差,则( )
A.Dξ1>Dξ2
B.Dξ1=Dξ2
C.Dξ1<Dξ2
D.Dξ1与Dξ2的大小关系与x1、x2、x3、x4的取值有关
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知双曲线C1:2x2﹣y2=1.
(1)过C1的左顶点引C1的一条渐近线的平行线,求该直线与另一条渐近线及x轴围成的三角形的面积;
(2)设斜率为1的直线l交C1于P、Q两点,若l与圆x2+y2=1相切,求证:OP⊥OQ;
(3)设椭圆C2:4x2+y2=1,若M、N分别是C1、C2上的动点,且OM⊥ON,求证:O到直线MN的距离是定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在空间直角坐标系中有直三棱柱ABC﹣A1B1C1 , CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为( )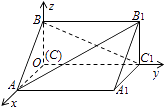
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”,利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值![]() ,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出
,这就是著名的“徽率”,如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出![]() 的值为 ( )
的值为 ( )
(参考数据:![]() )
)
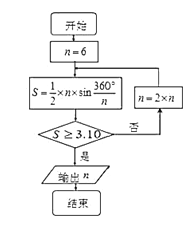
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com