
如图所示,已知抛物线E:y2=x与圆M:(x-4)2+y2=r2(r>0)相交于A、B、C、D四个点.
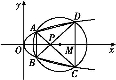
(1)求r的取值范围;
(2)当四边形ABCD的面积最大时,求对角线AC、BD的交点P的坐标.
(1)(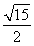 ,4) (2)(
,4) (2)( ,0)
,0)
【解析】
解:(1)将y2=x代入(x-4)2+y2=r2,
并化简得x2-7x+16-r2=0,①
E与M有四个交点的充要条件是方程①有两个不等的正根x1,x2,
由此得
解得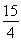 <r2<16.
<r2<16.
又r>0,
所以r的取值范围是(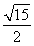 ,4).
,4).
(2)不妨设E与M的四个交点的坐标为:
A(x1, )、B(x1,-
)、B(x1,-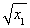 )、C(x2,-
)、C(x2,-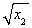 )、D(x2,
)、D(x2,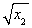 ).
).
则直线AC、BD的方程分别为
y-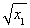 =
= ·(x-x1),
·(x-x1),
y+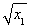 =
=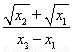 (x-x1),
(x-x1),
解得点P的坐标为(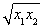 ,0).
,0).
设t=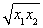 ,
,
由t=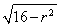 及(1)知0<t<
及(1)知0<t<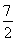 .
.
由于四边形ABCD为等腰梯形,
因而其面积S=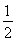 (2
(2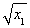 +2
+2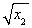 )·|x2-x1|.
)·|x2-x1|.
则S2=(x1+x2+2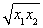 )[(x1+x2)2-4x1x2].
)[(x1+x2)2-4x1x2].
将x1+x2=7,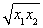 =t代入上式,
=t代入上式,
并令f(t)=S2,
得f(t)=(7+2t)2·(7-2t)(0<t<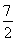 ).
).
求导数,f′(t)=-2(2t+7)(6t-7),
令f′(t)=0得t=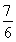 ,t=-
,t=-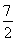 (舍去),
(舍去),
当0<t<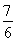 时,f′(t)>0;
时,f′(t)>0;
当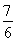 <t<
<t<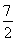 时,f′(t)<0.
时,f′(t)<0.
故当且仅当t=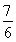 时,f(t)有最大值,
时,f(t)有最大值,
即四边形ABCD的面积最大.
故所求的点P的坐标为( ,0).
,0).


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:
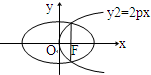
 如图所示,已知抛物线y2=2px(p>0)的焦点恰好是椭圆
如图所示,已知抛物线y2=2px(p>0)的焦点恰好是椭圆| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
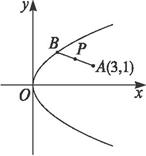
 如图所示,已知抛物线C1:x2=y,圆M:x2+(y-4)2=1,点P是抛物线C1上一点(异于原点),过点P作圆M的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程.
如图所示,已知抛物线C1:x2=y,圆M:x2+(y-4)2=1,点P是抛物线C1上一点(异于原点),过点P作圆M的两条切线,交抛物线C1于A,B两点,若过M,P两点的直线l垂直于AB,求直线l的方程.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省无锡市洛社高中高二(上)10月段考数学试卷(解析版) 题型:填空题
 的右焦点F,且两条曲线的交点连线也过焦点F,则该椭圆的离心率为 .
的右焦点F,且两条曲线的交点连线也过焦点F,则该椭圆的离心率为 .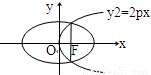
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com