
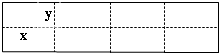
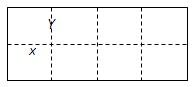
 解:(1)设小网箱的长、宽分别为x米、y米,筛网总长度为S,
解:(1)设小网箱的长、宽分别为x米、y米,筛网总长度为S,| 27 |
| 2 |
| 6xy |
|
|
| 15 |
| 4 |
| 15 |
| 2 |
| 20 |
| x |
| 15 |
| 2 |
| 8 |
| 3 |
| 15 |
| 4 |
| 20 |
| x |
| 20 |
| x |
| 16 |
| x |
| 8 |
| 3 |
| 15 |
| 4 |
| 15 |
| 4 |
| 15 |
| 4 |
| 16 |
| 3 |
| 15 |
| 4 |
| 16 |
| 3 |


科目:高中数学 来源:2015届辽宁省东北育才双语学校高一下学期期中考试数学试卷(解析版) 题型:解答题
如图所示是某水产养殖厂的养殖大网箱的平面图,四周的实线为网衣,为避免混养,
(1)若大网箱的面积为108平方米,每个小网箱的横边 、纵边
、纵边 设计为多少米时,才能使围成的网箱中筛网的总长度最小?
设计为多少米时,才能使围成的网箱中筛网的总长度最小?
(2)若大网箱的面积为160平方米,网衣的造价为112元/米,筛网的造价为96元/米,且大网箱的长与宽都不超过15米,则小网箱的横、纵边分别为多少米时,可使总造价最低?
查看答案和解析>>
科目:高中数学 来源:2012-2013学年福建安溪一中、养正中学高三上学期期中联考文数学试卷(解析版) 题型:解答题
(本小题满分12分)如图所示是某水产养殖场的养殖大网箱的平面图,四周的实线为网衣,为避免混养,用筛网(图中虚线)把大网箱隔成大小一样的小网箱.
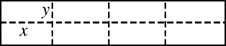
(1)若大网箱的面积为108平方米,每个小网箱的长x,宽y设计为多少米时,才能使围成的网箱中筛网总长度最小;
(2)若大网箱的面积为160平方米,网衣的造价为112元/米,筛网的造价为96元/米,且大网箱的长与宽都不超过15米,则小网箱的长、宽为多少米时,可使总造价最低?
查看答案和解析>>
科目:高中数学 来源:2010-2011学年江西省高三第三次段考数学理卷 题型:解答题
(本小题满分12分)如图所示是某水产养殖场的养殖大网箱的平面图,四周的实线为网衣,为避免混养,用筛网(图中虚线)把大网箱隔成大小一样的小网箱。
(1)若大网箱的面积为108平方米,每个小网箱的长x,宽y设计为多少米时,才能使围成的网箱中筛网总长度最小;
(2)若大网箱的面积为160平方米,网衣的造价为112元/米,筛网的造价为96元/米,且大网箱的长与宽都不超过15米,则小网箱的长、宽为多少米量,可使总造价最低?

查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示是某水产养殖厂的养殖大网箱的平面图,四周的实线为网衣,为避免混养,
(1)若大网箱的面积为108平方米,每个小网箱的横边![]() 、纵边
、纵边![]() 设计为多少米时,才能使围成的网箱中筛网的总长度最小?
设计为多少米时,才能使围成的网箱中筛网的总长度最小?
(2)若大网箱的面积为160平方米,网衣的造价为112元/米,筛网的造价为96元/米,且大网箱的长与宽都不超过15米,则小网箱的横、纵边分别为多少米时,可使总造价最低?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com