
如图所示,点O为做简谐运动的物体的平衡位置,取向右的方向为物体位移的正方向,若已知振幅为3 cm,周期为3 s,且物体向右运动到A点(距平衡位置最远处)开始计时.(1)求物体离开平衡位置的位移x(cm)和时间t(s)之间的函数关系式;(2)求该物体在t=5 s时的位置.
(1)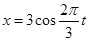 ;(2)O点左侧且距O点1.5 cm处.
;(2)O点左侧且距O点1.5 cm处.
解析试题分析:(1)根据正弦型函数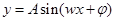 的物理模型为简谐运动.,因此可设所求函数解析式为
的物理模型为简谐运动.,因此可设所求函数解析式为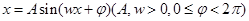 ,根据
,根据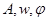 分别表示简谐运动的振幅,周期,初相的物理意义,与条件中描述的振幅为3cm,周期为3s以及距平衡位置最远处开始计时可求得
分别表示简谐运动的振幅,周期,初相的物理意义,与条件中描述的振幅为3cm,周期为3s以及距平衡位置最远处开始计时可求得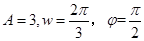 ,从而得到函数表达式为
,从而得到函数表达式为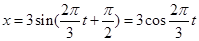 ;(2)在(1)中求得的函数表达式中令t=5,可得x=-1.5,即可求得物体在t=5s时的位置.
;(2)在(1)中求得的函数表达式中令t=5,可得x=-1.5,即可求得物体在t=5s时的位置.
(1)设位移x(cm)和时间t(s)之间的函数关系式为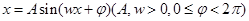 ,
,
则由已知条件,振幅为3cm,周期为3s可得,A=3,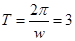 ,得
,得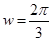 .
.
又∵物体向右运动到A点(距平衡位置最远处)开始计时,∴当t=0时,有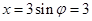 ,∴
,∴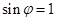 ,又∵
,又∵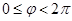 ,∴
,∴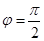 ,从而所求的函数关系式是
,从而所求的函数关系式是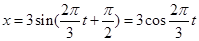 ;
;
(2)令t=5,得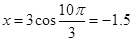 ,故该物体在t=5 s时的位置是在O点左侧且距O点1.5 cm处..
,故该物体在t=5 s时的位置是在O点左侧且距O点1.5 cm处..
考点:正弦型函数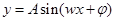 的物理模型简谐运动.
的物理模型简谐运动.


科目:高中数学 来源: 题型:解答题
如图,单位圆(半径为1的圆)的圆心O为坐标原点,单位圆与y轴的正半轴交于点A,与钝角α的终边OB交于点B(xB,yB),设∠BAO=β.
(1)用β表示α;
(2)如果 sin β=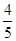 ,求点B(xB,yB)坐标;
,求点B(xB,yB)坐标;
(3)求xB-yB的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
函数f(x)=6cos2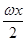 +
+ sin ωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.
sin ωx-3(ω>0)在一个周期内的图象如图所示,A为图象的最高点,B,C为图象与x轴的交点,且△ABC为正三角形.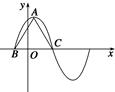
(1)求ω的值及函数f(x)的值域;
(2)若f(x0)=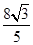 ,且x0∈
,且x0∈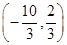 ,求f(x0+1)的值.
,求f(x0+1)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com