
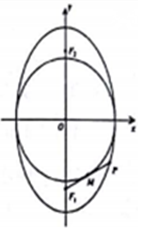
 若F1,F2是椭圆C:$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{m}$=1(0<m<9)的两个焦点,椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点M.
若F1,F2是椭圆C:$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{m}$=1(0<m<9)的两个焦点,椭圆上存在一点P,满足以椭圆短轴为直径的圆与线段PF1相切于该线段的中点M.分析 (Ⅰ)求出a=3,b=$\sqrt{m}$,设椭圆的下焦点F1,设线段PF1的中点为:M;由题意,OM⊥PF1,又OM=b,OM是△PF1F2的中位线,由椭圆定义,在Rt△OMF1中的勾股定理,求出b=2,得到m.然后求解椭圆C的方程.
(Ⅱ)上焦点坐标(0,$\sqrt{5}$).直线l的斜率k必存在.设A(x1,y1)B(x2,y2),弦AB的中点Q(x0,y0),利用平方差法得到AB的斜率,通过(1)当x0≠0时,k=kAB=$\frac{{y}_{0}-\sqrt{5}}{{x}_{0}}$,推出9x02+4y02-4$\sqrt{5}$y0=0,连结BN,则E为△ABN的重心,设E(x,y),利用重心坐标公式,推出$\left\{\begin{array}{l}{{x}_{0}=4x}\\{{y}_{0}=\frac{3}{2}y}\end{array}\right.$代入9x02+4y02-4$\sqrt{5}$y0=0轨迹方程,(2)当x0=0时,验证即可.
解答 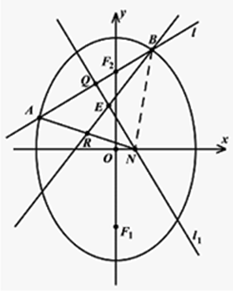 解:(Ⅰ)∵0<m<9,∴a=3,b=$\sqrt{m}$,不妨设椭圆的下焦点F1,设线段PF1的中点为:M;
解:(Ⅰ)∵0<m<9,∴a=3,b=$\sqrt{m}$,不妨设椭圆的下焦点F1,设线段PF1的中点为:M;
由题意,OM⊥PF1,又OM=b,OM是△PF1F2的中位线,
∴|PF2|=2b,
由椭圆定义,|PF1|=2a-2b=6-2b.∴$|M{F}_{1}|=\frac{1}{2}|P{F}_{1}|$=3-b,
在Rt△OMF1中:$|O{F}_{1}{|}^{2}=|OM{|}^{2}+|M{F}_{1}{|}^{2}$,
∴c2=b2+(3-b)2,又c2=a2-b2=9-b2.,
∴b2+(3-b)2=9-b2交点b=0(舍去)或b=2,∴m=b2=4.
∴椭圆C的方程:$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{4}$=1.
(Ⅱ)由(Ⅰ)椭圆C的方程:$\frac{{y}^{2}}{9}$+$\frac{{x}^{2}}{4}$=1.
上焦点坐标(0,$\sqrt{5}$).直线l的斜率k必存在.
设A(x1,y1)B(x2,y2),弦AB的中点Q(x0,y0),
由$\left\{\begin{array}{l}{{{4x}_{1}}^{2}+9{{y}_{1}}^{2}=36}\\{4{{x}_{2}}^{2}+9{{y}_{2}}^{2}=36}\end{array}\right.$,可得4(y1+y2)(y1-y2)=-9(x1+x2)(x1-x2),
∴k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{9({x}_{1}+{x}_{2})}{4({y}_{1}+{y}_{2})}$=-$\frac{9{x}_{0}}{4{y}_{0}}$(y0≠0)
(1)当x0≠0时,k=kAB=$\frac{{y}_{0}-\sqrt{5}}{{x}_{0}}$∴k=$-\frac{9{x}_{0}}{4{y}_{0}}$=$\frac{{y}_{0}-\sqrt{5}}{{x}_{0}}$⇒9x02+4y02-4$\sqrt{5}$y0=0,•
又l1:y-y0=$\frac{4{y}_{0}}{9{x}_{0}}(x-{x}_{0})$,∴N($-\frac{5}{4}{x}_{0},0$),
连结BN,则E为△ABN的重心,设E(x,y),
则$\left\{\begin{array}{l}{x=\frac{{x}_{1}+{x}_{2}+(-\frac{5}{4}{x}_{0})}{3}=\frac{{x}_{0}}{4}}\\{9=\frac{{y}_{1}+{y}_{2}+0}{3}=\frac{2{y}_{0}}{3}}\end{array}\right.$,
∴$\left\{\begin{array}{l}{{x}_{0}=4x}\\{{y}_{0}=\frac{3}{2}y}\end{array}\right.$代入9x02+4y02-4$\sqrt{5}$y0=0可得:48x2+3y2-2$\sqrt{5}y=0$,(y≠0).
(2)当x0=0时,l:y=$\sqrt{5}$,N(0,0),E(0,$\frac{2\sqrt{5}}{3}$)也适合上式,
综上所述,点E的轨迹方程为:48x2+3y2-2$\sqrt{5}y=0$,(y≠0).
点评 本题考查椭圆的简单性质以及椭圆方程的求法,直线与椭圆的位置关系的综合应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
 如图,在六面体ABCD-A1B1C1D1中,平面ABCD∥平面A1B1C1D1,DD1∥平面A1B1BA,DD1∥平面B1BCC1.
如图,在六面体ABCD-A1B1C1D1中,平面ABCD∥平面A1B1C1D1,DD1∥平面A1B1BA,DD1∥平面B1BCC1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,+∞) | B. | (0,+∞) | C. | (1,+∞) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1] | B. | (-∞,2] | C. | (-∞,3] | D. | [-1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
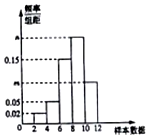 有一个容量为100的样本,其频率分布直方图如图所示,已知样本数据落在区间[10,12)内的频数比样本数据落在区间[8,10)内的频数少12,则实数m的值等于( )
有一个容量为100的样本,其频率分布直方图如图所示,已知样本数据落在区间[10,12)内的频数比样本数据落在区间[8,10)内的频数少12,则实数m的值等于( )| A. | 0.10 | B. | 0.11 | C. | 0.12 | D. | 0.13 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
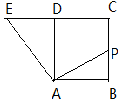 如图,四边形ABCD是正方形,延长CD至E,使得DE=CD,若点P为BC的中点,且$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ=( )
如图,四边形ABCD是正方形,延长CD至E,使得DE=CD,若点P为BC的中点,且$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ=( )| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{5}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com