
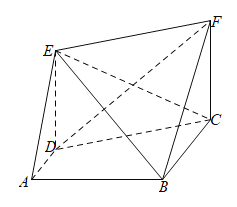
【题目】如图,圆柱的轴截面ABCD是边长为2的正方形,点P是圆弧CD上的一动点(不与C,D重合),点Q是圆弧AB的中点,且点P,Q在平面ABCD的两侧.
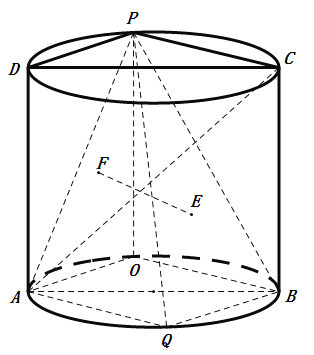
(1)证明:平面PAD⊥平面PBC;
(2)设点P在平面ABQ上的射影为点O,点E,F分别是△PQB和△POA的重心,当三棱锥P﹣ABC体积最大时,回答下列问题.
(i)证明:EF∥平面PAQ;
(ii)求平面PAB与平面PCD所成二面角的正弦值.
【答案】(1)见解析(2)(i)见解析(ii)![]() .
.
【解析】
(1)证明AD⊥PC, PC⊥PD,得到PC⊥平面PAD,得到证明.
(2)连接PE并延长交BQ于点M,连接PF并延长交OA于点N,连接MN,证明EF∥AQ得到答案;以O为坐标原点,OA,OB,OP所在直线为x,y,z轴建立空间直角坐标系,平面PAB的法向量![]() ,平面PCD的法向量
,平面PCD的法向量![]() ,计算夹角得到答案.
,计算夹角得到答案.
(1)证明:因为ABCD是轴截面,所以AD⊥平面PCD,所以AD⊥PC,
又点P是圆弧CD上的一动点(不与C,D重合),且CD为直径,所以PC⊥PD,
又AD∩PD=D,PD平面PAD,AD平面PAD,所以PC⊥平面PAD,
PC平面PBC,故平面PAD⊥平面PBC;
(2)当三棱锥P﹣ABC体积最大时,点P为圆弧CD的中点,
所以点O为圆弧AB的中点,所以四边形AQBO为正方形,且OP⊥AB,
(i)证明:连接PE并延长交BQ于点M,连接PF并延长交OA于点N,连接MN,
则MN∥AQ,因为E,F分别为三角形的重心,所以EF∥MN,
所以EF∥AQ,又AQ平面PAQ,EF![]() 平面PAQ,所以EF∥平面PAQ;
平面PAQ,所以EF∥平面PAQ;
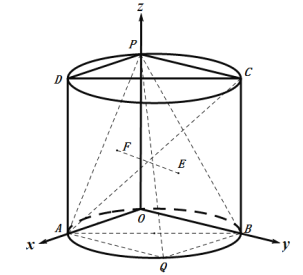
(ii)以O为坐标原点,OA,OB,OP所在直线为x,y,z轴建立空间直角坐标系,如图,则P(0,0,2),A(![]() ,0,0),B(0,
,0,0),B(0,![]() ,0),
,0),
![]() ,
,![]() ,
,
设平面PAB的法向量![]() \,则
\,则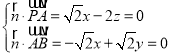 ,
,
可取![]() ,又平面PCD的法向量
,又平面PCD的法向量![]() ,
,
所以cos![]() ,
,
所以平面PAB与平面PCD所成二面角的正弦值为![]() .
.



科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),其中
为参数),其中![]() .以原点为极点,
.以原点为极点, ![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求出曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点,记点
两点,记点![]() ,
, ![]() 相应的参数分别为
相应的参数分别为![]() ,
, ![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.卷八中第33问:“今有三角果一垛,底阔每面七个.问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为( )
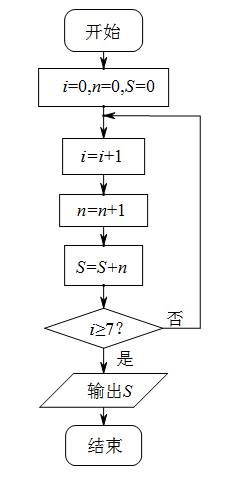
A.28B.56C.84D.120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设s,t是不相等的两个正数,且s+slnt=t+tlns,则s+t﹣st的取值范围为( )
A.(﹣∞,1)B.(﹣∞,0)C.(0,+∞)D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 三个班共有
三个班共有![]() 名学生,为调查他们的上网情况,通过分层抽样获得了部分学生一周的上网时长,数据如下表(单位:小时):
名学生,为调查他们的上网情况,通过分层抽样获得了部分学生一周的上网时长,数据如下表(单位:小时):
|
|
|
|
|
|
(1)试估计![]() 班的学生人数;
班的学生人数;
(2)从这120名学生中任选1名学生,估计这名学生一周上网时长超过15小时的概率;
(3)从A班抽出的6名学生中随机选取2人,从B班抽出的7名学生中随机选取1人,求这3人中恰有2人一周上网时长超过15小时的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,若椭圆经过点
,若椭圆经过点![]() ,且△PF1F2的面积为2.
,且△PF1F2的面积为2.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设斜率为1的直线![]() 与以原点为圆心,半径为
与以原点为圆心,半径为![]() 的圆交于A,B两点,与椭圆C交于C,D两点,且
的圆交于A,B两点,与椭圆C交于C,D两点,且![]() (
(![]() ),当
),当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列![]() 的公差
的公差![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,满足
,满足![]() ,且
,且![]() ,
,![]() .若实数
.若实数![]() ,则称
,则称![]() 具有性质
具有性质![]() .
.
(1)请判断![]() 、
、![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)设![]() 为数列
为数列![]() 的前
的前![]() 项和,
项和,![]() ,且
,且![]()
![]() 恒成立.求证:对任意的
恒成立.求证:对任意的![]()
![]() ,实数
,实数![]() 都不具有性质
都不具有性质![]() ;
;
(3)设![]() 是数列
是数列![]() 的前
的前![]() 项和,若对任意的
项和,若对任意的![]() ,
,![]() 都具有性质
都具有性质![]() ,求所有满足条件的
,求所有满足条件的![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,
为矩形,![]() ,平面
,平面![]() 平面
平面![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成二面角的正弦值;
所成二面角的正弦值;
(3)若点![]() 在线段
在线段![]() 上,且直线
上,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com