
【题目】如图,在三棱锥S﹣ABC中,SA⊥底面ABC,AC=AB=SA=2,AC⊥AB,D、E分别是AC、BC的中点,F在SE上,且SF=2FE.
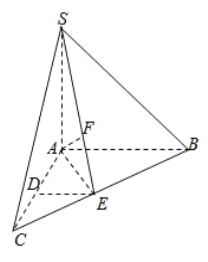
(1)求证:平面SBC⊥平面SAE
(2)若G为DE中点,求二面角G﹣AF﹣E的大小.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)利用![]() 底面
底面![]() 证得
证得![]() ,由等腰三角形的性质证得
,由等腰三角形的性质证得![]() ,由此证得
,由此证得![]() 平面
平面![]() ,进而证得平面
,进而证得平面![]() 平面
平面![]() .
.
(2)以![]() 为坐标原点建立空间直角坐标系,通过平面
为坐标原点建立空间直角坐标系,通过平面![]() 和平面
和平面![]() 的法向量,计算出二面角
的法向量,计算出二面角![]() 的余弦值,进而求得二面角的大小.
的余弦值,进而求得二面角的大小.
(1)∵SA⊥底面ABC,∴SA⊥BC,
又∵AC=AB,且点E是BC的中点,
∴BC⊥AE,
∵SA∩AE=A,∴BC⊥底面SAE,
∵BC平面SBC,
∴平面SBC⊥平面SAE.
(2)以A点为坐标原点,分别以AC,AB,AS为x,y,z轴建立空间坐标系O﹣xyz,
则A(0,0,0),S(0,0,2),E(1,1,0),G(1,![]() ,0),C(2,0,0),B(0,2,0),
,0),C(2,0,0),B(0,2,0),
由SF=2FE得F(![]() ,
,![]() ,
,![]() ),
),
∴![]() =(1,1,0),
=(1,1,0),![]() =(
=(![]()
![]() ,
,![]() ),
),![]() =(1,
=(1,![]() ,0),
,0),![]() =(2,﹣2,0).
=(2,﹣2,0).
设平面AFG的法向量为![]() =(x,y,z),则
=(x,y,z),则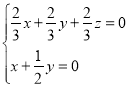 ,
,
令y=2,得到x=﹣1,z=﹣1,
即![]() =(﹣1,2,﹣1),
=(﹣1,2,﹣1),
设平面AFE的法向量为![]() ,
,
由(1)知![]() 为平面AES的一个法向量,
为平面AES的一个法向量,![]() =
=![]() =(2,﹣2,0),
=(2,﹣2,0),
∴cosα=![]() =
=![]() =
=![]() ,
,
∵二面角G﹣AF﹣E的平面角为锐角,
∴二面角G﹣AF﹣E的大小为![]() .
.



 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,过点![]() 的直线l与抛物线
的直线l与抛物线![]() 交于A,B两点,以AB为直径作圆,记为
交于A,B两点,以AB为直径作圆,记为![]() ,
,![]() 与抛物线C的准线始终相切.
与抛物线C的准线始终相切.
(1)求抛物线C的方程;
(2)过圆心M作x轴垂线与抛物线相交于点N,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)若函数![]() 在定义域上单调增,求
在定义域上单调增,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 在定义域上不单调,试判定
在定义域上不单调,试判定![]() 的零点个数,并给出证明过程.
的零点个数,并给出证明过程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 上两点,圆
上两点,圆![]() .
.
(1)若![]() 轴,且满足直线
轴,且满足直线![]() 与圆
与圆![]() 相切,求圆
相切,求圆![]() 的方程;
的方程;
(2)若圆![]() 的半径为2,点
的半径为2,点![]() ,
,![]() 满足
满足![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得弦长的最大值.
截得弦长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,斜三棱柱![]() 中,
中,![]() 是边长为2的正三角形,
是边长为2的正三角形,![]() 为
为![]() 的中点,
的中点,![]() 平面
平面![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,
,![]() 为
为![]() 与
与![]() 的交点,且
的交点,且![]() 与平面
与平面![]() 所成的角为
所成的角为![]() .
.
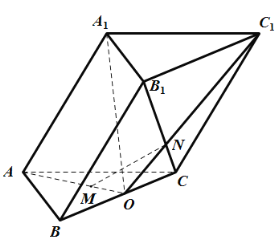
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年新冠肺炎疫情暴发以来,中国政府迅速采取最全面、最严格、最彻底的防控举措,坚决遏制疫情蔓延势头,努力把疫情影响降到最低,为全世界抗击新冠肺炎疫情做岀了贡献.为普及防治新冠肺炎的相关知识,某高中学校开展了线上新冠肺炎防控知识竞答活动,现从大批参与者中随机抽取200名幸运者,他们的得分(满分100分)数据统计结果如图:
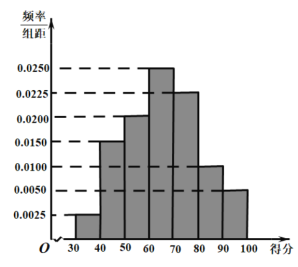
(1)若此次知识竞答得分![]() 整体服从正态分布,用样本来估计总体,设
整体服从正态分布,用样本来估计总体,设![]() ,
,![]() 分别为这200名幸运者得分的平均值和标准差(同一组数据用该区间中点值代替),求
分别为这200名幸运者得分的平均值和标准差(同一组数据用该区间中点值代替),求![]() ,
,![]() 的值(
的值(![]() ,
,![]() 的值四舍五入取整数),并计算
的值四舍五入取整数),并计算![]() ;
;
(2)在(1)的条件下,为感谢大家积极参与这次活动,对参与此次知识竞答的幸运者制定如下奖励方案:得分低于![]() 的获得1次抽奖机会,得分不低于
的获得1次抽奖机会,得分不低于![]() 的获得2次抽奖机会.假定每次抽奖中,抽到18元红包的概率为
的获得2次抽奖机会.假定每次抽奖中,抽到18元红包的概率为![]() ,抽到36元红包的概率为
,抽到36元红包的概率为![]() .已知高三某同学是这次活动中的幸运者,记
.已知高三某同学是这次活动中的幸运者,记![]() 为该同学在抽奖中获得红包的总金额,求
为该同学在抽奖中获得红包的总金额,求![]() 的分布列和数学期望,并估算举办此次活动所需要抽奖红包的总金额.
的分布列和数学期望,并估算举办此次活动所需要抽奖红包的总金额.
参考数据:![]() ;
;![]() ;
;![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体![]() 中,
中,![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 上一点,
上一点,![]() ,
,![]() ,
,![]() .动点
.动点![]() 在上底面
在上底面![]() 上,且满足三棱锥
上,且满足三棱锥![]() 的体积等于1,则直线
的体积等于1,则直线![]() 与
与![]() 所成角的正切值的最大值为( )
所成角的正切值的最大值为( )

A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市旅游管理部门为提升该市26个旅游景点的服务质量,对该市26个旅游景点的交通、安全、环保、卫生、管理五项指标进行评分,每项评分最低分0分,最高分100分,每个景点总分为这五项得分之和,根据考核评分结果,绘制交通得分与安全得分散点图、交通得分与景点总分散点图如下:
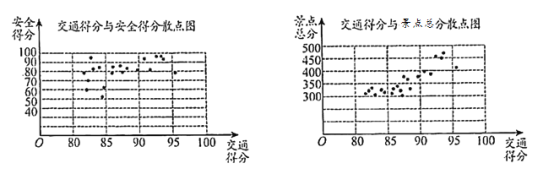
请根据图中所提供的信息,完成下列问题:
(I)若从交通得分前6名的景点中任取2个,求其安全得分都大于90分的概率;
(II)若从景点总分排名前6名的景点中任取3个,记安全得分不大于90分的景点个数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(III)记该市26个景点的交通平均得分为![]() 安全平均得分为
安全平均得分为![]() ,写出
,写出![]() 和
和![]() 的大小关系?(只写出结果)
的大小关系?(只写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com