
【题目】下图是某地5月1日至15日日平均温度变化的折线图,日平均温度高于20度低于27度时适宜户外活动,某人随机选择5月1日至5月14日中的某一天到达该地停留两天(包括到达当日).
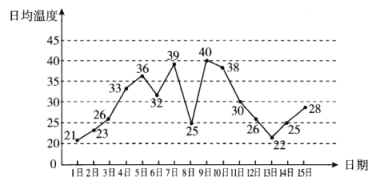
(1)求这15天日平均温度的极差和均值;
(2)求此人停留期间只有一天的日平均温度适宜户外活动的概率;
(3)由折线图判断从哪天开始连续三天日平均温度的方差最大?(写出结论,不要求证明)
【答案】(1)19度,29.6度;(2)![]() ;(3)从5月7日开始连续三天的日平均温度方差最大.
;(3)从5月7日开始连续三天的日平均温度方差最大.
【解析】
(1)由折线图读出所有数据,最高温度40度,最低温度为21度,即可求出极差,利用求平均数的公式直接求平均数;
(2)由折线图可以得到只有一天的日平均温度适宜户外活动共有3-4日,7-8日,8-9日,11-12日,14-15日这5种情况,然后利用求古典概型的概率的公式求解
(3)连续3天数据波动最大的,则方差最大
解:(1)由折线图最高日平均温度40度,最低温度21度,故日平均温度的极差为![]() 度,
度,
设日平均温度的均值为![]() ,则
,则
![]() 度
度
(2)由题意此人停留的可能时间有14种情况,
只有一天的日平均温度适宜户外活动共有3-4日,7-8日,8-9日,11-12日,14-15日这5种情况,
故概率![]() .
.
(3)从5月7日开始连续三天的日平均温度方差最大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】如图所示的多面体中,AD⊥平面PDC,四边形ABCD为平行四边形,E为AD的中点,F为线段PB上的一点,∠CDP=120°,AD=3,AP=5,![]() .
.
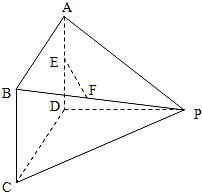
(Ⅰ)试确定点F的位置,使得直线EF∥平面PDC;
(Ⅱ)若PB=3BF,求直线AF与平面PBC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了积极稳妥疫情期间的复学工作,市教育局抽调5名机关工作人员去某街道3所不同的学校开展驻点服务,每个学校至少去1人,若甲、乙两人不能去同一所学校,则不同的分配方法种数为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,一动圆与直线
,一动圆与直线![]() 相切且与圆
相切且与圆![]() 外切.
外切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若经过定点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,
两点, ![]() 是线段
是线段![]() 的中点,过
的中点,过![]() 作
作![]() 轴的平行线与曲线
轴的平行线与曲线![]() 相交于点
相交于点![]() ,试问是否存在直线
,试问是否存在直线![]() ,使得
,使得![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某社区组织“学习强国”的知识竞赛,从参加竞赛的市民中抽出40人,将其成绩分成以下6组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,第6组
,第6组![]() ,得到如图所示的频率分布直方图.现采用分层抽样的方法,从第2,3,4组中按分层抽样抽取8人,则第2,3,4组抽取的人数依次为( )
,得到如图所示的频率分布直方图.现采用分层抽样的方法,从第2,3,4组中按分层抽样抽取8人,则第2,3,4组抽取的人数依次为( )
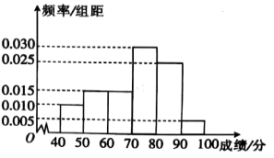
A.1,3,4B.2,3,3C.2,2,4D.1,1,6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com