
【题目】已知如图:平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G,H分别是DF,BE的中点. 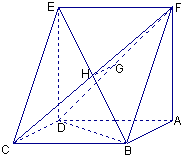
(1)求证:GH∥平面CDE;
(2)若CD=2,DB=4 ![]() ,求四棱锥F﹣ABCD的体积.
,求四棱锥F﹣ABCD的体积.
【答案】
(1)证明:∵EF∥AD,AD∥BC,∴EF∥BC且EF=AD=BC
∴四边形EFBC是平行四边形,∴H为FC的中点
又∵G是FD的中点
∴HG∥CD
∵HG平面CDE,CD平面CDE
∴GH∥平面CDE
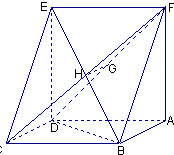
(2)解:∵平面ADEF⊥平面ABCD,交线为AD
且FA⊥AD,∴FA⊥平面ABCD.
∵BC=6,∴FA=6
又∵CD=2,DB=4 ![]() ,CD2+DB2=BC2
,CD2+DB2=BC2
∴BD⊥CD
∴SABCD=CD×BD=8 ![]()
∴VF﹣ABCD= ![]() ×SABCD×FA=
×SABCD×FA= ![]() ×
× ![]() ×6=16
×6=16 ![]()
【解析】(1)证明GH∥平面CDE,利用线面平行的判定定理,只需证明HG∥CD;(2)证明FA⊥平面ABCD,求出SABCD,即可求得四棱锥F﹣ABCD的体积.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】天气预报说,在今后的三天中,每一天下雨的概率均为40%.现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨;再以每三个随机数作为一组,代表这三天的下雨情况.经随机模拟试验产生了如下20组随机数: 907 966 191 925 271 932 812 458 569 683
431 257 393 027 556 488 730 113 537 989
据此估计,这三天中恰有两天下雨的概率近似为( )
A.0.35
B.0.25
C.0.20
D.0.15
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在数列{an}中,a1+2a2++22a3+…2n﹣1an=(n2n﹣2n+1)t对任意n∈N*成立,其中常数t>0.若关于n的不等式 ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() >
> ![]() 的解集为{n|n≥4,n∈N*},则实数m的取值范围是 .
的解集为{n|n≥4,n∈N*},则实数m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足:对于任意n∈N*且n≥2时,an+λan﹣1=2n+1,a1=4.
(1)若 ![]() ,求证:{an﹣3n}为等比数列;
,求证:{an﹣3n}为等比数列;
(2)若λ=﹣1.①求数列{an}的通项公式; ②是否存在k∈N*,使得 ![]() +25为数列{an}中的项?若存在,求出所有满足条件的k的值;若不存在,请说明理由.
+25为数列{an}中的项?若存在,求出所有满足条件的k的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点P是圆O:x2+y2=1与x轴正半轴的交点,半径OA在x轴的上方,现将半径OA绕原点O逆时针旋转 ![]() 得到半径OB.设∠POA=x(0<x<π),
得到半径OB.设∠POA=x(0<x<π), ![]() .
. 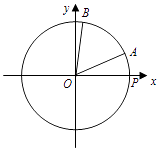
(1)若 ![]() ,求点B的坐标;
,求点B的坐标;
(2)求函数f(x)的最小值,并求此时x的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列{an}的前n项和为Sn , 且an=2﹣2Sn , 数列{bn}为等差数列,且b5=14,b7=20.
(1)求数列{an}的通项公式;
(2)若cn=anbn , n∈N* , 求数列{cn}的前n项和Tn .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com