，
.求:(I) 函数
的最大值及取得最大值的自变量
的集合；
(II) 函数
的单调增区间.
本小题考查三角公式、三角函数的性质及已知三角函数值求角等基础知识，考查综合运用三角函数有关知识的能力.
(Ⅰ)解法一：∵f（x）=
=2+sin2x+cos2x
=2+sin（2x+）
∴当2x+=2kπ+，即x=kπ+
（k∈Z）时,f（x）取得最大值2+
.
因此f（x）取得最大值的自变量x的集合是{x|x=kπ+
，k∈Z}.
解法二：∵f（x）=（sin2x·cos2x）+ sin2x +2cos2x
=1+sin2x+1+cos2x
=2+
sin（2x+
）.
∴当2x+
=2kπ+
，即x=kπ+
（k∈Z）时f（x）取得最大值2+
.
因此,f（x）取得最大值的自变量x的集合是{x|x=kπ+
，k∈Z}.
(Ⅱ)解：f（x）=2+
sin（2x+
）,
由题意得2kπ-
≤2x+
≤2kπ+
（k∈Z）.即
kπ-
.
阅读快车系列答案科目：高中数学 来源： 题型：044
(2007
辽宁，17)已知函数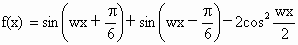
，
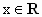(其中w＞0)．
(1)
求函数f(x)的值域；(2)
若对任意的a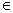
R，函数y=f(x)，x
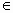(a，a＋π]的图象与直线y=－1有且仅有两个不同的交点，试确定w的值(不必证明)，并求函数y=f(x)，xR的单调增区间．查看答案和解析>>
科目：高中数学 来源： 题型：044
(2006
福建，17)已知函数为
，x
R．
(1)
求函数f(x)的最小正周期和单调增区间；(2)
函数f(x)的图象可以由函数y=sin 2x(xR)的图象经过怎样的变换得到?查看答案和解析>>
科目：高中数学 来源： 题型：044
(2006
山东，17)已知函数
，且y=f(x)的最大值为2，其图象相邻两对称轴间的距离为2，并过点(1，2)．
(1)
求φ；(2)
计算f(1)＋f(2)＋…＋f(2008)．查看答案和解析>>
科目：高中数学 来源： 题型：044
(2005
江西，17)已知函数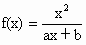
(a、b为常数)，且方程f(x)－x＋12=0有两个实根为
，
．
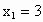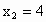(1)
求函数f(x)的解析式；(2)
设k＞1，解关于x的不等式：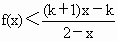
．查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com