
分析 (1)①由抛物线方程得到焦点坐标,写出AB所在直线方程,与抛物线方程联立,利用根与系数的关系可得y1y2为定值,并求出此定值;
②由抛物线的焦半径公式把|AF|、|BF|用A,B的纵坐标及p表示,代入后结合根与系数的关系整理得答案;
③取AB的中点M,分别过A、B、M作准线的垂线AA′、BB′、MN,垂足分别为A′、B′、N,作出图形,利用抛物线的定义及梯形的中位线性质可推导,|MN|=$\frac{1}{2}$|AB|,从而可判断圆与准线的位置关系;
④由抛物线方程求出抛物线的焦点坐标,由斜截式写出过焦点的直线方程,和抛物线方程联立求出A,B两点横坐标的积,再利用导数写出过A,B两点的切线方程,然后整体运算可求得两切线的交点的纵坐标为定值$-\frac{p}{2}$,从而得到两切线交点在抛物线的准线上;
(2)由题意求出A,B的坐标,设出Q的坐标,由导数求出抛物线在Q点的切线方程,再求出PA、PB的直线方程,联立求出D,E的坐标,把△QAB与△PDE的面积都用Q点的横坐标表示后得答案;
(3)设出两点G、H两点坐标,得到直线GH方程x=-ky+m,把直线GH方程与抛物线方程联立,化为一元二次方程,由韦达定理求出GH中点,应用中点在对称轴上,且判别式大于0,可求出k的取值范围.
解答 (1)证明:①根据抛物线方程,得F(0,$\frac{p}{2}$),直线AB的方程为y=kx+$\frac{p}{2}$.
联立抛物线方程得x2-2pkx-p2=0.
∴x1x2=-p2,则y1y2=$\frac{{{x}_{1}}^{2}}{2p}•\frac{{{x}_{2}}^{2}}{2p}=\frac{{p}^{4}}{4{p}^{2}}$=$\frac{{p}^{2}}{4}$.
∴y1y2为定值,定值为$\frac{{p}^{2}}{4}$;
②根据抛物线的定义,|AF|=y1+$\frac{p}{2}$,|BF|=y2+$\frac{p}{2}$;
∴$\frac{1}{|AF|}+\frac{1}{|BF|}$=$\frac{1}{{y}_{1}+\frac{p}{2}}$+$\frac{1}{{y}_{2}+\frac{p}{2}}$=$\frac{4({y}_{1}+{y}_{2})+4p}{4{y}_{1}{y}_{2}+2p({y}_{1}+{y}_{2})+{p}^{2}}$;
y1y2=$\frac{{p}^{2}}{4}$代入化简可得:$\frac{1}{|AF|}+\frac{1}{|BF|}$=$\frac{4({y}_{1}+{y}_{2})+4p}{4•\frac{{p}^{2}}{4}+2p({y}_{1}+{y}_{2})+{p}^{2}}=\frac{4({y}_{1}+{y}_{2})+4p}{2{p}^{2}+2p({y}_{1}+{y}_{2})}$=$\frac{2}{p}$;
即$\frac{1}{|AF|}+\frac{1}{|BF|}$为定值,定值为$\frac{2}{p}$;
③取AB的中点M,分别过A、B、M作准线的垂线AA′、BB′、MN,垂足分别为A′、B′、N,如图所示:
由抛物线的定义可知,|AA′|=|AF|,|BB′|=|BF|,
在直角梯形APQB中,|MN|=$\frac{1}{2}$(|AA′|+|BB′|)=$\frac{1}{2}$(|AF|+|BF|)=$\frac{1}{2}$|AB|,
故圆心M到准线的距离等于半径,
∴以AB为直径的圆与抛物线的准线相切;
④抛物线方程可化为$y=\frac{1}{2p}{x}^{2}$,于是$y′=\frac{1}{p}x$,
∴${k}_{AT}=\frac{1}{p}{x}_{1},{k}_{BT}=\frac{1}{p}{x}_{2}$,直线AT的方程为y-y1=$\frac{{x}_{1}}{p}(x-{x}_{1})$,即y$-\frac{{{x}_{1}}^{2}}{2p}=\frac{{x}_{1}}{p}(x-{x}_{1})$,$y=\frac{{x}_{1}}{p}x-\frac{{{x}_{1}}^{2}}{2p}$,
同理,直线BT的方程为$y=\frac{{x}_{2}}{p}x-\frac{{{x}_{2}}^{2}}{2p}$.
联立$\left\{\begin{array}{l}{y=\frac{{x}_{1}}{p}x-\frac{{{x}_{1}}^{2}}{2p}}\\{y=\frac{{x}_{2}}{p}x-\frac{{{x}_{2}}^{2}}{2p}}\end{array}\right.$,解得$y=\frac{\frac{{x}_{1}{{x}_{2}}^{2}}{2p}-\frac{{x}_{2}{{x}_{1}}^{2}}{2p}}{{x}_{2}-{x}_{1}}=\frac{\frac{{x}_{1}{x}_{2}}{2p}({x}_{2}-{x}_{1})}{{x}_{2}-{x}_{1}}$=$\frac{1}{2p}•(-{p}^{2})=-\frac{p}{2}$.
∴两条切线的交点一定在准线上;
(2)解:如图,
当p=2时,抛物线C的方程为x2=4y,联立直线y=1,可得A(-2,1),B(2,1),
设Q(${x}_{0},\frac{1}{4}{{x}_{0}}^{2}$),则过Q的切线方程为y-$\frac{1}{4}{{x}_{0}}^{2}=\frac{1}{2}{x}_{0}(x-{x}_{0})$,即$y=\frac{1}{2}{x}_{0}x-\frac{1}{4}{{x}_{0}}^{2}$.
又P(0,-1),
∴PA、PB所在直线方程分别为$\frac{y+1}{1+1}=\frac{x-0}{-2-0},\frac{y+1}{1+1}=\frac{x-0}{2-0}$,即x+y+1=0,x-y-1=0.
联立$\left\{\begin{array}{l}{x+y+1=0}\\{y=\frac{1}{2}{x}_{0}x-\frac{1}{4}{{x}_{0}}^{2}}\end{array}\right.$,解得D($\frac{{x}_{0}-2}{2},-\frac{{x}_{0}}{2}$),
联立$\left\{\begin{array}{l}{x-y-1=0}\\{y=\frac{1}{2}{x}_{0}x-\frac{1}{4}{{x}_{0}}^{2}}\end{array}\right.$,解得E($\frac{{x}_{0}+2}{2},\frac{{x}_{0}}{2}$).
∴${S}_{△QAB}=\frac{1}{2}×4×(1-\frac{1}{4}{{x}_{0}}^{2})$=$2(1-\frac{{{x}_{0}}^{2}}{4})$,
${S}_{△PDE}=\frac{1}{2}×(1-\frac{1}{4}{{x}_{0}}^{2})×|{x}_{D}-{x}_{E}|$=$\frac{1}{2}(1-\frac{1}{4}{{x}_{0}}^{2})|\frac{{x}_{0}-2}{2}-\frac{{x}_{0}+2}{2}|$=$1-\frac{1}{4}{{x}_{0}}^{2}$.
故△QAB与△PDE的面积之比为2;
(3)解:设两点G、H关于直线y=kx+1对称,故可设直线GH方程为y=-$\frac{1}{k}$x+m,代入y=x2,
得:x2+$\frac{1}{k}$x-m=0.
设G(x1,y1)、H(x2,y2),则GH中点K(x0,y0),则x0=$\frac{{x}_{1}+{x}_{2}}{2}=-\frac{1}{2k}$,y0=$\frac{1}{2{k}^{2}}$+m.
∵点M(x0,y0)在直线y=kx+1上,
∴$\frac{1}{2{k}^{2}}$+m=k(-$\frac{1}{2k}$)+1,
∴m=$\frac{1}{2}-\frac{1}{2{k}^{2}}$.
又∵GH与抛物线交于不同两点,∴△=$\frac{1}{{k}^{2}}$+4m>0.
把m代入得$\frac{1}{{k}^{2}}$+4($\frac{1}{2}-\frac{1}{2{k}^{2}}$)>0,化简得$\frac{1}{{k}^{2}}$<2,解得k<-$\frac{\sqrt{2}}{2}$或k>$\frac{\sqrt{2}}{2}$.
故k的取值范围是(-∞,-$\frac{\sqrt{2}}{2}$)∪($\frac{\sqrt{2}}{2},+∞$).
点评 本题考查直线与抛物线的位置关系、直线与圆的位置关系,考查抛物线的定义,考查了轨迹方程,训练了利用导数研究曲线上某点处的切线方程,考查了整体运算思想方法,是难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 设a,b∈N*,记R(a\b)为a除以b所得的余数,执行如图所示的程序框图,若输入a=243,b=45,则输出的值等于( )
设a,b∈N*,记R(a\b)为a除以b所得的余数,执行如图所示的程序框图,若输入a=243,b=45,则输出的值等于( )| A. | 0 | B. | 1 | C. | 9 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 63 | B. | 31 | C. | 15 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
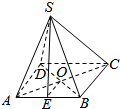 如图,S-ABCD是正四棱锥,已知底面边长AB=6cm,侧棱SA=3$\sqrt{5}$cm,求该正四棱锥的侧面SAB的斜高SE和底面AC所成角的大小.
如图,S-ABCD是正四棱锥,已知底面边长AB=6cm,侧棱SA=3$\sqrt{5}$cm,求该正四棱锥的侧面SAB的斜高SE和底面AC所成角的大小.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 质量指标值分组 | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) |
| 频数 | 2 | 3 | 4 | 5 | 4 | 2 |
| 质量指标值分组 | [10,20) | [20,30) | [30,40) | [40,50) | [50,60) | [60,70) |
| 频数 | 0.15 | 0.2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 3 | C. | 8 | D. | 11 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com