
【题目】四面体ABCD的每个顶点都在球O的表面上,AB是球O的一条直径,且AC=2,BC=4,现有下面四个结论:
①球O的表面积为20π;②AC上存在一点M,使得AD∥BM;
③若AD=3,则BD=4;④四面体ABCD体积的最大值为![]() .
.
其中所有正确结论的编号是( )
A.①②B.②④C.①④D.①③④
科目:高中数学 来源: 题型:
【题目】2019年12月以来,湖北省武汉市持续开展流感及相关疾病监测,发现多起病毒性肺炎病例,均诊断为病毒性肺炎/肺部感染,后被命名为新型冠状病毒肺炎(CoronaVirusDisease2019,COVID—19),简称“新冠肺炎”.下图是2020年1月15日至1月24日累计确诊人数随时间变化的散点图.
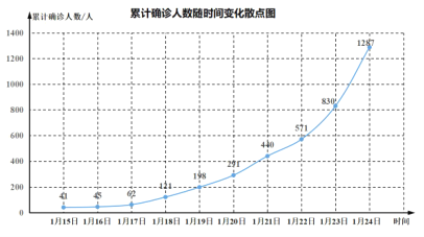
为了预测在未釆取强力措施下,后期的累计确诊人数,建立了累计确诊人数y与时间变量t的两个回归模型,根据1月15日至1月24日的数据(时间变量t的值依次1,2,…,10)建立模型![]() 和
和![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个适宜作为累计确诊人数y与时间变量t的回归方程类型?(给出判断即可,不必说明理由)
哪一个适宜作为累计确诊人数y与时间变量t的回归方程类型?(给出判断即可,不必说明理由)
(2根据(1)的判断结果及附表中数据,建立y关于x的回归方程;
(3)以下是1月25日至1月29日累计确诊人数的真实数据,根据(2)的结果回答下列问题:
时间 | 1月25日 | 1月26日 | 1月27日 | 1月28日 | 1月29日 |
累计确诊人数的真实数据 | 1975 | 2744 | 4515 | 5974 | 7111 |
(ⅰ)当1月25日至1月27日这3天的误差(模型预测数据与真实数据差值的绝对值与真实数据的比值)都小于0.1则认为模型可靠,请判断(2)的回归方程是否可靠?
(ⅱ)2020年1月24日在人民政府的强力领导下,全国人民共同采取了强力的预防“新冠肺炎”的措施,若采取措施5天后,真实数据明显低于预测数据,则认为防护措施有效,请判断预防措施是否有效?
附:对于一组数据(![]() ,
,![]() ,……,
,……,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为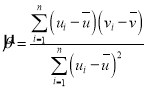 ,
,![]() .
.
参考数据:其中![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
5.5 | 390 | 19 | 385 | 7640 | 31525 | 154700 | 100 | 150 | 225 | 338 | 507 |
查看答案和解析>>
科目:高中数学 来源: 题型:
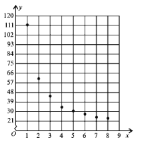
【题目】2019年,中国的国内生产总值(GDP)已经达到100亿元人民币,位居世界第二,这其中实体经济的贡献功不可没,实体经济组织一般按照市场化原则运行,某生产企业一种产品的成本由原料成本及非原料成本组成,每件产品的非原料成本![]() (元)与生产该产品的数量
(元)与生产该产品的数量![]() (千件)有关,经统计得到如下数据:
(千件)有关,经统计得到如下数据:

根据以上数据绘制了如下的散点图
现考虑用反比例函数模型![]() 和指数函数模型
和指数函数模型![]() 分别对两个变量关系进行拟合,为此变换如下:令
分别对两个变量关系进行拟合,为此变换如下:令![]() ,则
,则![]() ,即
,即![]() 与
与![]() 也满足线性关系,令
也满足线性关系,令![]() ,则
,则![]() ,即
,即![]() 也满足线线关系,这样就可以使用最小二乘法求得非线性回归方程,已求得用指数函数模型拟合的回归方程为
也满足线线关系,这样就可以使用最小二乘法求得非线性回归方程,已求得用指数函数模型拟合的回归方程为![]() 与
与![]() 的相关系数
的相关系数![]() ,其他参考数据如下(其中
,其他参考数据如下(其中![]() )
)

(1)求指数函数模型和反比例函数模型中![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)试计算![]() 与
与![]() 的相关系数
的相关系数![]() ,并用相关系数判断:选择反比例函数和指数函数两个模型中哪一个拟合效果更好(精确到0.01)?
,并用相关系数判断:选择反比例函数和指数函数两个模型中哪一个拟合效果更好(精确到0.01)?
(3)根据(2)小题的选择结果,该企业采用订单生产模式(即根据订单数量进行生产,产品全部售出),根据市场调研数据,该产品定价为100元时得到签到订单的情况如下表:
订单数(千件) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
概率 |
|
|
|
|
|
|
|
|
|
|
|
已知每件产品的原来成本为10元,试估算企业的利润是多少?(精确到1千元)
参考公式:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别是:
的斜率和截距的最小二乘估计分别是: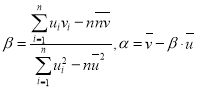 相关系数:
相关系数: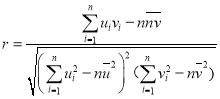
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在①![]() ;②
;②![]() ,这两个条件中任选一个,补充在下面问题中,然后解答补充完整的题目.
,这两个条件中任选一个,补充在下面问题中,然后解答补充完整的题目.
在![]() 中,内角
中,内角![]() 的对边分别为
的对边分别为![]() ,设
,设![]() 的面积为
的面积为![]() ,已知 .
,已知 .
(1)求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值.
的值.
注:如果选择多个条件分别解答,按第一个解答计分.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等.问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,丙所得为( )
A.![]() 钱B.1钱C.
钱B.1钱C.![]() 钱D.
钱D.![]() 钱
钱
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,
,![]() 为椭圆
为椭圆![]() 的右焦点,且椭圆
的右焦点,且椭圆![]() 上的点到
上的点到![]() 的距离的最小值为
的距离的最小值为![]() ,过
,过![]() 作直线
作直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,点
两点,点 .
.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在这样的直线![]() ,使得以
,使得以![]() ,
,![]() 为邻边的平行四边形为矩形?若存在,求出直线
为邻边的平行四边形为矩形?若存在,求出直线![]() 的斜率;若不存在,请说明理由.
的斜率;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种新型嫁接巨丰葡萄,在新疆地区种植一般亩产不低于5千斤,产量高的达到上万斤.受嫁接年限的影响,其产量一般逐年衰减,若在新疆地区平均亩产量低于5千斤,则从新嫁接.以下是新疆某地区从2014年开始嫁接后每年的平均亩产量y(单位:千斤)的数据表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号x | 1 | 2 | 3 | 4 | 5 |
平均亩产量y | 8.2 | 7.8 | 7.2 | 6.6 | 5.4 |
(1)求y关于x的线性回归方程;
(2)利用(1)中的回归直线方程,预计哪一年开始从新嫁接.
附:回归直线的斜率和截距的最小二乘法估计公式分别为: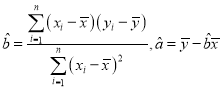 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com