
【题目】设定义在D上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,当
,当![]() 时,若
时,若![]() 在D内恒成立,则称P点为函数
在D内恒成立,则称P点为函数![]() 的“类对称中心点”,则函数
的“类对称中心点”,则函数![]() 的“类对称中心点”的坐标是________.
的“类对称中心点”的坐标是________.
【答案】![]()
【解析】
由求导公式求出函数f(x)的导数,由导数的几何意义和条件求出切线方程,再求出y=g(x),设F(x)=f(x)﹣g(x),求出导数化简后利用分类讨论和导数与函数单调性的关系,判断出F(x)的单调性和最值,从而可判断出![]() 的符号,再由“类对称中心点”的定义确定“类对称中心点”的坐标.
的符号,再由“类对称中心点”的定义确定“类对称中心点”的坐标.
解:由题意得,f′(x)![]() ,f(x0)
,f(x0)![]() (x>0),
(x>0),
即函数y=f(x)的定义域D=(0,+∞),
所以函数y=f(x)在点P(x0,f(x0))处的切线方程l方程为:
y﹣(![]() )=(
)=(![]() )(x﹣x0),
)(x﹣x0),
则g(x)=(![]() )(x﹣x0)+(
)(x﹣x0)+(![]() ),
),
设F(x)=f(x)﹣g(x)![]() lnx﹣[(
lnx﹣[(![]() )(x﹣x0)+(
)(x﹣x0)+(![]() )],
)],
则F(x0)=0,
所以F′(x)=f′x)﹣g′(x)![]() (
(![]() )
)![]()
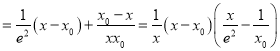
当0<x0<e时,F(x)在(x0,![]() )上递减,
)上递减,
∴x∈(x0,![]() )时,F(x)<F(x0)=0,此时
)时,F(x)<F(x0)=0,此时![]() ,
,
当x0>e时,F(x)在(![]() ,x0)上递减;
,x0)上递减;
∴x∈(![]() ,x0)时,F(x)>F(x0)=0,此时
,x0)时,F(x)>F(x0)=0,此时![]() ,
,
∴y=F(x)在(0,e)∪(e,+∞)上不存在“类对称点”.
若x0=e,![]() 0,则F(x)在(0,+∞)上是增函数,
0,则F(x)在(0,+∞)上是增函数,
当x>x0时,F(x)>F(x0)=0,当x<x0时,F(x)<F(x0)=0,
故![]() ,
,
即此时点P是y=f(x)的“类对称点”,
综上可得,y=F(x)存在“类对称点”,e是一个“类对称点”的横坐标,
又f(e)![]() ,所以函数f(x)的“类对称中心点”的坐标是
,所以函数f(x)的“类对称中心点”的坐标是![]() ,
,
故答案为:![]() .
.


 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:高中数学 来源: 题型:
【题目】至![]() 年底,我国发明专利申请量已经连续
年底,我国发明专利申请量已经连续![]() 年位居世界首位,下表是我国
年位居世界首位,下表是我国![]() 年至
年至![]() 年发明专利申请量以及相关数据.
年发明专利申请量以及相关数据.
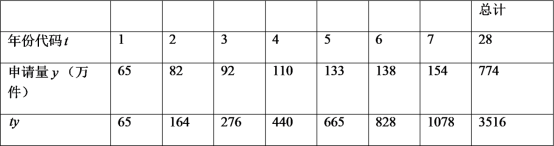
注:年份代码![]() ~
~![]() 分别表示
分别表示![]() ~
~![]() .
.
(1)可以看出申请量每年都在增加,请问这几年中哪一年的增长率达到最高,最高是多少?
(2)建立![]() 关于
关于![]() 的回归直线方程(精确到
的回归直线方程(精确到![]() ),并预测我国发明专利申请量突破
),并预测我国发明专利申请量突破![]() 万件的年份.
万件的年份.
参考公式:回归直线的斜率和截距的最小二乘法估计分别为 ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的几何体中,四边形ABCD是正方形,PA⊥平面ABCD,E,F分别是线段AD,PB的中点,PA=AB=1.
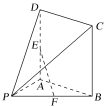
(1)证明:EF∥平面PDC;
(2)求点F到平面PDC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数集![]() (
(![]() ,
,![]() )具有性质
)具有性质![]() :对任意的
:对任意的![]() 、
、![]() (
(![]() ),
),![]() 与
与![]() 两数中至少有一个属于
两数中至少有一个属于![]() .
.
(1)分别判断数集![]() 与
与![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)证明:![]() ,且
,且![]() ;
;
(3)证明:当![]() 时,
时,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 成等比数列.
成等比数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知在四棱锥S﹣AFCD中,平面SCD⊥平面AFCD,∠DAF=∠ADC=90°,AD=1,AF=2DC=4,![]() ,B,E分别为AF,SA的中点.
,B,E分别为AF,SA的中点.
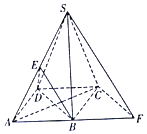
(1)求证:平面BDE∥平面SCF
(2)求二面角A﹣SC﹣B的余弦值
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com