
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)讨论![]() 单调区间;
单调区间;
(Ⅱ)若直线![]() 是函数
是函数![]() 图象的切线,求
图象的切线,求![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
【题目】某种植园在芒果临近成熟时,随机从一些芒果树上摘下100个芒果,其质量分别在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:克)中,经统计得频率分布直方图如图所示.
(单位:克)中,经统计得频率分布直方图如图所示.
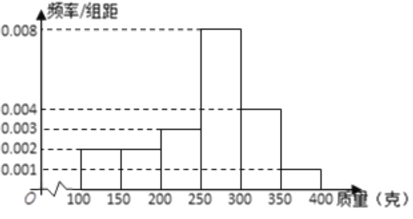
(1) 经计算估计这组数据的中位数;
(2)现按分层抽样从质量为![]() ,
,![]() 的芒果中随机抽取
的芒果中随机抽取![]() 个,再从这
个,再从这![]() 个中随机抽取
个中随机抽取![]() 个,求这
个,求这![]() 个芒果中恰有
个芒果中恰有![]() 个在
个在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的个数为( )
①两个有共同始点且相等的向量,其终点可能不同;
②若非零向量![]() 与
与![]() 共线,则
共线,则![]() 、
、![]() 、
、![]() 、
、![]() 四点共线;
四点共线;
③若非零向量![]() 与
与![]() 共线,则
共线,则![]() ;
;
④四边形![]() 是平行四边形,则必有
是平行四边形,则必有![]() ;
;
⑤![]() ,则
,则![]() 、
、![]() 方向相同或相反.
方向相同或相反.
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某亲子游戏结束时有一项抽奖活动,抽奖规则是:盒子里面共有4个小球,小球上分别写有0,1,2,3的数字,小球除数字外其他完全相同,每对亲子中,家长先从盒子中取出一个小球,记下数字后将小球放回,孩子再从盒子中取出一个小球,记下小球上数字将小球放回.抽奖活动的奖励规则是:①若取出的两个小球上数字之积大于4,则奖励飞机玩具一个;②若取出的两个小球上数字之积在区间上![]() ,则奖励汽车玩具一个;③若取出的两个小球上数字之积小于1,则奖励饮料一瓶.
,则奖励汽车玩具一个;③若取出的两个小球上数字之积小于1,则奖励饮料一瓶.
(1)求每对亲子获得飞机玩具的概率;
(2)试比较每对亲子获得汽车玩具与获得饮料的概率,哪个更大?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
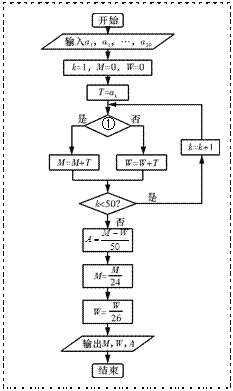
【题目】在一次“汉马”(武汉马拉松比赛的简称)全程比赛中,50名参赛选手(24名男选手和26名女选手)的成绩(单位:分钟)分别为数据![]() (成绩不为0).
(成绩不为0).
(Ⅰ)24名男选手成绩的茎叶图如图⑴所示,若将男选手成绩由好到差编为1~24号,再用系统抽样方法从中抽取6人,求其中成绩在区间![]() 上的选手人数;
上的选手人数;

(Ⅱ)如图⑵所示的程序用来对这50名选手的成绩进行统计.为了便于区别性别,输入时,男选手的成绩数据用正数,女选手的成绩数据用其相反数(负数),请完成图⑵中空白的判断框①处的填写,并说明输出数值![]() 和
和![]() 的统计意义.
的统计意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于研究性学习的需要,中学生李华持续收集了手机“微信运动”团队中特定20名成员每天行走的步数,其中某一天的数据记录如下:
5860 6520 7326 6798 7325 8430 8215 7453 7446 6754
7638 6834 6460 6830 9860 8753 9450 9860 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表(设步数为![]() )
)
组别 | 步数分组 | 频数 |
|
| 2 |
|
| 10 |
|
|
|
|
| 2 |
|
|
|
(Ⅰ)写出![]() 的值,并回答这20名“微信运动”团队成员一天行走步数的中位数落在哪个组别;
的值,并回答这20名“微信运动”团队成员一天行走步数的中位数落在哪个组别;
(Ⅱ)记![]() 组步数数据的平均数与方差分别为
组步数数据的平均数与方差分别为![]() ,
,![]() ,
,![]() 组步数数据的平均数与方差分别为
组步数数据的平均数与方差分别为![]() ,
,![]() ,试分别比较
,试分别比较![]() 与以
与以![]() ,
,![]() 与
与![]() 的大小;(只需写出结论)
的大小;(只需写出结论)
(Ⅲ)从上述![]() 两个组别的数据中任取2个数据,记这2个数据步数差的绝对值为
两个组别的数据中任取2个数据,记这2个数据步数差的绝对值为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com