
分析 (1)分类讨论,利用奇偶函数定义判断.
(2)求解导数f′(x)=2ax$+\frac{4}{{X}^{2}}$=$\frac{2a{x}^{3}+4}{{x}^{2}}$,讨论得出当f′(x)≥0时,x≤$\root{3}{-\frac{2}{a}}$,当f′(x)≤0时,x≥$\root{3}{-\frac{2}{a}}$,根据a∈(-2,-1),判断$-\frac{2}{a}$∈(1,2),得出导数的符号即可.
解答 解:(1)函数f(x)=ax2-$\frac{4}{x}$,其中a为常数,
①当a=0时,f(x)=-$\frac{4}{x}$是奇函数,
∵f(-x)=-$\frac{4}{-x}$=$\frac{4}{x}$=-f(-x)
∴当a=0时,f(x)=-$\frac{4}{x}$是奇函数,
②∵当a≠0时,f(x)=-$\frac{4}{x}$是非奇非偶函数,
f(-x)≠-f(-x),f(-x)≠f(-x)
∴当a≠0时,f(x)=-$\frac{4}{x}$是非奇非偶函数,
(2)∵函数f(x)在($\frac{1}{2}$,1)上的单调性,
∴f′(x)=2ax$+\frac{4}{{X}^{2}}$=$\frac{2a{x}^{3}+4}{{x}^{2}}$,
当f′(x)≥0时,x≤$\root{3}{-\frac{2}{a}}$,当f′(x)≤0时,x≥$\root{3}{-\frac{2}{a}}$,
∵a∈(-2,-1),∴$-\frac{2}{a}$∈(1,2),
∴$\root{3}{-\frac{2}{a}}$>1,
在($\frac{1}{2}$,1)上f′(x)>0,
∴函数f(x)在($\frac{1}{2}$,1)上的单调递增函数.
点评 本题综合考查了函数性质,导数在解决函数综合问题中的运用,属于中档题,关键单调与导数的关系.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=-x3,x∈R | B. | y=x2,x∈R | C. | y=x,x∈R | D. | $y={({\frac{1}{2}})^x}$,x∈R |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 6 | C. | 8 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 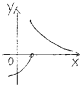 | B. | 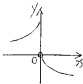 | C. | 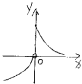 | D. | 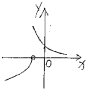 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com