
����Ŀ����֪����x��һԪ���κ���f��x����ax2��2bx+8��
��1���輯��P��{1��2��3}��Q��{2��3��4��5}���ֱ�Ӽ���P��Q�����ȡһ������Ϊa��b������y��f��x�������䣨������2]���������Ϊ�������ĸ��ʣ�
��2���輯��P��[1��3]��Q[2��5]���ֱ�Ӽ���P��Q�����ȡһ��ʵ����Ϊa��b������y��f��x�������䣨������2]���������Ϊ�������ĸ��ʣ�
���𰸡���1��![]() ����2��
����2��![]() ��
��
��������
(1)�����оٷ���Ϲŵ���͵ĸ��ʹ�ʽ���м��㼴��;
(2)��������ʽ���Ӧ������,�����Ӧ��������,��ϼ��θ��͵ĸ��ʹ�ʽ���м��㼴��.
(1)���¼���n=3��4=12,
������y=f(x)������(����,2]���������������,��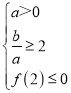 ,
,
������������a,bΪ(1,3),(1,4),(1,5),(2,4),(2,5),����5��,
���Ӧ�ĸ���P![]() ;
;
(2)����������֪![]() ,
,
��y=f(x)������(����,2]���������������,
��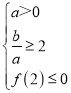 ,��
,��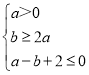 ,
,
��Ӧ����������ͼ��ʾ:
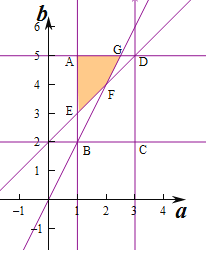
��![]() ��
��![]() ,��F(2,4),
,��F(2,4),
��![]() ��
��![]() ,��E(1,3),
,��E(1,3),
��![]() ��
��![]() ,��G(
,��G(![]() ,5),
,5),
��A(1,5),D(3,5),
����Ӱ���ֵ����S=S��AED��S��GDF![]() 2��2
2��2![]() (3
(3![]() )(5��4)=2
)(5��4)=2![]() ,
,
����ABCD�����S=2��3=6,
���Ӧ�ĸ���![]() .
.


 ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() �����ų�һ�ţ�����������£����ж����ֲ�ͬ�ŷ���
�����ų�һ�ţ�����������£����ж����ֲ�ͬ�ŷ���
��1���ײ������ˣ�
��2���ס��ҡ�������������һ��
��3���ס��ұ�����һ���Ҽס��Ҷ�����������ڣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x������kx+![]() ��ex��2x����f��x����0�Ľ⼯������ֻ��һ������������ʵ��k��ȡֵ��ΧΪ ��������
��ex��2x����f��x����0�Ľ⼯������ֻ��һ������������ʵ��k��ȡֵ��ΧΪ ��������
A. [![]() ��
��![]() ��B. ��
��B. ��![]() ��
��![]() ]
]
C. [![]() ��D. [
��D. [![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() ����
����![]() ��ֵ��
��ֵ��
��2����֪ij���![]() �ˣ�����
�ˣ�����![]() ������������������ͬ�ĸ���Ϊ
������������������ͬ�ĸ���Ϊ![]() ��
��![]() ����һ�꿴��365��.
����һ�꿴��365��.
��i����![]() �ı���ʽ��
�ı���ʽ��
��ii������![]() �Ľ���ֵ����ȷ��0.01��.
�Ľ���ֵ����ȷ��0.01��.
�ο���ֵ��![]() ��
��![]() ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ȡ����һ��ʱ����������һ����Ʒ������һ������ָ��ֵ����������ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ.
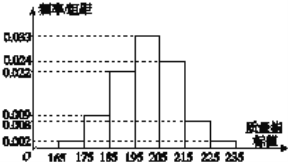
��1�������������ƽ��ֵ![]() ������
������![]() ����ͬһ���е������ø���������е�ֵ��������
����ͬһ���е������ø���������е�ֵ��������
��2��������ָ��ֵ��![]() ֮��Ϊһ��Ʒ.
֮��Ϊһ��Ʒ.
��i���������������壬�ʸù���һ�������IJ�Ʒ�Ƿ���![]() ����Ϊһ��Ʒ��
����Ϊһ��Ʒ��
��ii��ij�����ϡ�����ֱ�����50����Ʒ���������ı��������������ݣ��ж��Ƿ���![]() �İ�����Ϊһ��Ʒ��������ʱ���йأ�
�İ�����Ϊһ��Ʒ��������ʱ���йأ�
һ��Ʒ���� | ��һ��Ʒ���� | �ܼ� | |
���� | 36 | 50 | |
���� | 26 | 50 | |
�ܼ� |
����![]() .
.
| 0.25 | 0.15 | 0.10 | 0.050 | 0.010 | 0.001 |
| 1.323 | 2.072 | 2.706 | 3.841 | 6.635 | 10.828 |
�ο����ݣ�![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������C��x2=4y�Ľ���ΪF������P��-2��2����ֱ��l��������C����A��B���㣮
��1������PΪA��B���е�ʱ����ֱ��AB�ķ��̣�
��2����|AF||BF|����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������12�֣���1��С��5�֣���2��С��7����
��ͼ����Բ![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ��
��![]() ��ֱ�߽���Բ��
��ֱ�߽���Բ��![]() ���㣬��
���㣬��![]()

��1����![]() ������Բ�ı�����
������Բ�ı�����
��2����![]() ����Բ��������
����Բ��������![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��0����a��1������P������f��x����logax�ڣ�0��+������Ϊ������������Q������g��x����x2��2ax+4����㣮
��1��������P��Q����P��Q�٣���ʵ��a��ȡֵ��Χ��
��2������S������y��f��g��x����������[2��+������ֵ��Ϊ������������SΪ�����⣬��ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ������ABCD�У�AB��CD����BAD��90����AB��AD��1��CD��2��������BCD����BD��������BC'D��ʹ��AD��BC'��

��1����֤��ƽ��C'BD��ƽ��ABD��
��2����C'D��ƽ��ABC'���ɽǵ�����ֵ��
��3��MΪBD�е㣬������M��AC'��B������ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com