
【题目】设各项均为正数的数列{an}的前n项和为Sn , 且满足2 ![]() =an+1(n∈N*).
=an+1(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若bn=(an+1)2 ![]() ,求数列{bn}的前n项和Tn .
,求数列{bn}的前n项和Tn .
【答案】解:(Ⅰ)当n=1时,a1=S1 , 有2 ![]() =a1+1,解得a1=1; 当n≥2时,由2
=a1+1,解得a1=1; 当n≥2时,由2 ![]() =an+1得4Sn=an2+2an+1,4Sn﹣1=an﹣12+2an﹣1+1,
=an+1得4Sn=an2+2an+1,4Sn﹣1=an﹣12+2an﹣1+1,
两式相减得4an=an2﹣an﹣12+2(an﹣an﹣1),
所以(an+an﹣1)(an﹣an﹣1﹣2)=0,
因为数列{an}的各项为正,所以an﹣an﹣1﹣2=0,
所以数列{an}是以1为首项,2为公差的等差数列,
所以数列{an}的通项公式为an=2n﹣1.
(Ⅱ)由(Ⅰ)知bn=(an+1)2 ![]() =2n22n﹣1=n4n .
=2n22n﹣1=n4n .
所以前n项和Tn=14+242+343+…+n4n ,
4Tn=142+243+344+…+n4n+1 ,
两式相减得﹣3Tn=4+42+43+…+4n﹣n4n+1
= ![]() ﹣n4n+1 ,
﹣n4n+1 ,
化简可得Tn= ![]() +
+ ![]() 4n+1 .
4n+1 .
【解析】(Ⅰ)首先利用Sn与an的关系:当n=1时,a1=S1 , 当n≥2时,an=Sn﹣Sn﹣1;结合已知条件等式推出数列{an}是等差数列,由此求得数列{an}的通项公式;(Ⅱ)首先结合(Ⅰ)求得bn的表达式,然后利用错位相减法,结合等比数列的求和公式求解即可.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系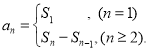 ),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.
),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
【题目】三国魏人刘徽,自撰《海岛算经》,专论测高望远.其中有一题:今有望海岛,立两表齐,高三丈,前後相去千步,令後表与前表相直.从前表却行一百二十三步,人目著地取望岛峰,与表末参合.从後表却行百二十七步,人目著地取望岛峰,亦与表末参合.问岛高几何?译文如下:要测量海岛上一座山峰A的高度AH,立两根高三丈的标杆BC和DE,前后两杆相距BD=1000步,使后标杆杆脚D与前标杆杆脚B与山峰脚H在同一直线上,从前标杆杆脚B退行123步到F,人眼著地观测到岛峰,A、C、F三点共线,从后标杆杆脚D退行127步到G,人眼著地观测到岛峰,A、E、G三点也共线,则山峰的高度AH=( ) 步(古制:1步=6尺,1里=180丈=1800尺=300步)
A.1250
B.1255
C.1230
D.1200
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直三棱柱ABC﹣A1BlC1中,平面α与棱AB,AC,A1C1 , A1B1分别交于点E,F,G,H,且直线AA1∥平面α.有下列三个命题:①四边形EFGH是平行四边形;②平面α∥平面BCC1B1;③平面α⊥平面BCFE.其中正确的命题有( )
A.①②
B.②③
C.①③
D.①②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,设![]() 为不同的两点,直线
为不同的两点,直线![]() 的方程为
的方程为![]() ,设
,设![]() ,其中
,其中![]() 均为实数.下列四个说法中:
均为实数.下列四个说法中:
①存在实数![]() ,使点
,使点![]() 在直线
在直线![]() 上;
上;
②若![]() ,则过
,则过![]() 两点的直线与直线
两点的直线与直线![]() 重合;
重合;
③若![]() ,则直线
,则直线![]() 经过线段
经过线段![]() 的中点;
的中点;
④若![]() ,则点
,则点![]() 在直线
在直线![]() 的同侧,且直线
的同侧,且直线![]() 与线段
与线段![]() 的延长线相交.
的延长线相交.
所有结论正确的说法的序号是______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)与y=F(x)的图象关于y轴对称,当函数y=f(x)和y=F(x)在区间[a,b]同时递增或同时递减时,把区间[a,b]叫做函数y=f(x)的“不动区间”.若区间[1,2]为函数f(x)=|2x﹣t|的“不动区间”,则实数t的取值范围是( )
A.(0,2]
B.[ ![]() ,+∞)
,+∞)
C.[ ![]() ,2]
,2]
D.[ ![]() ,2]∪[4,+∞)
,2]∪[4,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
分组 | 频数 | 频率 |
[10,15) | 10 | 0.25 |
[15,20) | 25 | n |
[20,25) | m | p |
[25,30) | 2 | 0.05 |
合计 | M | 1 |

(1)求出表中M,p及图中a的值;
(2)若该校高一学生有360人,试估计该校高一学生参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,请列举出所有基本事件,并求至多1人参加社区服务次数在区间[20,25)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M过C(1,-1),D(-1,1)两点,且圆心M在x+y-2=0上.
(1)求圆M的方程;
(2)设点P是直线3x+4y+8=0上的动点,PA,PB是圆M的两条切线,A,B为切点,求四边形PAMB面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长方体ABCD-A1B1C1D1中,AA1=AB=2,AD=1,点E、F、G分别是DD1、AB、CC1的中点.求异面直线A1E与GF所成角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com