练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．已知△ABC中，|$\overrightarrow{BC}$|=6，$\overrightarrow{AB}$•$\overrightarrow{AC}$=16．D为边BC的中点．则|$\overrightarrow{AD}$|=$\sqrt{15}$．

    分析 作图辅助，可得（$\overrightarrow{AB}$-$\overrightarrow{AC}$）2=36，|$\overrightarrow{AD}$|2=$\frac{1}{4}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$）2，从而解得．

    解答 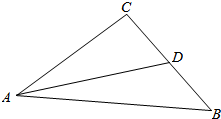解：∵|$\overrightarrow{BC}$|=6，
    ∴（$\overrightarrow{AB}$-$\overrightarrow{AC}$）2=36，
    ∴|$\overrightarrow{AD}$|2=$\frac{1}{4}$（$\overrightarrow{AB}$+$\overrightarrow{AC}$）2
    =$\frac{1}{4}$[（$\overrightarrow{AB}$-$\overrightarrow{AC}$）2+4$\overrightarrow{AB}$•$\overrightarrow{AC}$]
    =$\frac{1}{4}$（36+24）=15，
    故|$\overrightarrow{AD}$|=$\sqrt{15}$，
    故答案为：$\sqrt{15}$．

    点评 本题考查了平面向量的数量积与线性运算的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    20．福州为了迎接青运会，计划从2011年到2015年，每年年初投入资金用于更新和改进体育场所与设施，若2011年年初投入a万元，以后每年年初投入的资金比上一年递增10%，则投入的总资金约为（参考数据 1.14≈1.46，1.15≈1.61）（　　）
    A．4.6a万元B．6.1a万元C．14.6a万元D．16.1a万元

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知函数f（x）=|x-3|-|x+1|，命题p：关于x的不等式f（x）＞a对x∈R恒成立；命题q：函数y=x2-ax+4在区间[5，+∞）上单调递增．
    （1）解不等式f（x）≤0；
    （2）若命题“p或q”是真命题，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．如图，在多面体ABCDEF中，底面ABCD为菱形，∠BAD=60°，△ADE为等边三角形，且平面ADE⊥平面ABCD，EF $\stackrel{∥}{=}$$\frac{1}{2}$AB，点G为CD的中点．
    （Ⅰ）证明：BD⊥EG；
    （Ⅱ）求直线DE与平面BCF所成的角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+y2=1（a＞1）的左、上顶点分别为A、B，椭圆C的左焦点为F，且△ABF的面积为$\frac{2-\sqrt{3}}{2}$，则椭圆C的方程为$\frac{{x}^{2}}{4}+{y}^{2}=1$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．某开心农场要用一段长为40m的篱笆，围成一个矩形菜园ABCD，若设菜园的边长AB为xm，菜园的面积为ym2．
    （1）求y与x之间的函数关系式，写出x的取值范围；
    （2）当x为何值时，菜园面积最大？并求出最大值？

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．如图，某房地产公司要在一块矩形宽阔地面上开发物业，阴影部分是不能开发的古建筑群，且要求用在一条直线上的栏栅进行隔离，古建筑群的边界为曲线y=1-$\frac{4}{3}$x2的一部分，栏栅与矩形区域边界交于点M，N．则△MON面积的最小值为$\frac{2}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．设全集U=R，A={x|x2+px+12=0}，B={x|x2-5x+q=0}，若（∁UA）∩B={2}，求A∪B．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．若函数f（x）=2|x|-1，则函数g（x）=f（f（x））+ex的零点的个数是3．

    查看答案和解析>>

    同步练习册答案