
【题目】已知直线l:x+2y-2=0.
(1)求直线l1:y=x-2关于直线l对称的直线l2的方程;
(2)求直线l关于点A(1,1)对称的直线方程.
【答案】(1)7x-y-14=0;(2)x+2y-4=0.
【解析】
(1)先求出两直线的交点P(2,0),再求出![]() ,即得直线l2的方程;(2)直线l关于点A(1,1)对称的直线和直线l平行,所以设所求的直线方程为x+2y+m=0,求出m的值即得解.
,即得直线l2的方程;(2)直线l关于点A(1,1)对称的直线和直线l平行,所以设所求的直线方程为x+2y+m=0,求出m的值即得解.
(1)由![]() 解得交点P(2,0).
解得交点P(2,0).
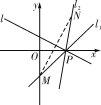
在l1上取点M(0,-2),
M关于l的对称点设为N(a,b),
则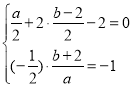 ,
,
解得![]() ,所以
,所以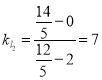 ,
,
又直线l2过点P(2,0),
所以直线l2的方程为7x-y-14=0.
(2)直线l关于点A(1,1)对称的直线和直线l平行,
所以设所求的直线方程为x+2y+m=0.
在l上取点B(0,1),则点B(0,1)关于点A(1,1)的对称点C(2,1)必在所求的直线上,
所以![]() ,所以m=-4,
,所以m=-4,
即所求的直线方程为x+2y-4=0.


科目:高中数学 来源: 题型:
【题目】在![]() 中,D,E分别为AB,AC的中点,
中,D,E分别为AB,AC的中点,![]() ,以DE为折痕将
,以DE为折痕将![]() 折起,使点A到达点P的位置,如图.
折起,使点A到达点P的位置,如图.

(1)证明:![]() ;
;
(2)若平面DEP![]() 平面BCED,求直线DC与平面BCP所成角的正弦值。
平面BCED,求直线DC与平面BCP所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“伦敦眼”坐落在英国伦敦泰晤士河畔,是世界上首座观景摩天轮,又称“千禧之轮”,该摩天轮的半径为6(单位:![]() ),游客在乘坐舱
),游客在乘坐舱![]() 升到上半空鸟瞰伦敦建筑
升到上半空鸟瞰伦敦建筑![]() ,伦敦眼与建筑之间的距离
,伦敦眼与建筑之间的距离![]() 为12(单位:
为12(单位:![]() ),游客在乘坐舱
),游客在乘坐舱![]() 看建筑
看建筑![]() 的视角为
的视角为![]() .
.

(1)当乘坐舱![]() 在伦敦眼的最高点
在伦敦眼的最高点![]() 时,视角
时,视角![]() ,求建筑
,求建筑![]() 的高度;
的高度;
(2)当游客在乘坐舱![]() 看建筑
看建筑![]() 的视角
的视角![]() 为
为![]() 时,拍摄效果最好.若在伦敦眼上可以拍摄到效果最好的照片,求建筑
时,拍摄效果最好.若在伦敦眼上可以拍摄到效果最好的照片,求建筑![]() 的最低高度.
的最低高度.
(说明:为了便于计算,数据与实际距离有误差,伦敦眼的实际高度为![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区某农产品近几年的产量统计如表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份代码t | 1 | 2 | 3 | 4 | 5 | 6 |
年产量y(万吨) | 6.6 | 6.7 | 7 | 7.1 | 7.2 | 7.4 |
(Ⅰ)根据表中数据,建立![]() 关于的线性回归方程
关于的线性回归方程![]() ;
;
(Ⅱ)根据线性回归方程预测2019年该地区该农产品的年产量.
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: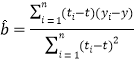 ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留小数点后两位)
,计算结果保留小数点后两位)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某客运公司用![]() 、
、![]() 两种型号的车辆承担甲、乙两地的长途客运业务,每车每天往返一次.
两种型号的车辆承担甲、乙两地的长途客运业务,每车每天往返一次.![]() 、
、![]() 两种型号的车辆的载客量分别是32人和48人,从甲地到乙地的营运成本依次为1500元/辆和2000元/辆.公司拟组建一个不超过21辆车的车队,并要求
两种型号的车辆的载客量分别是32人和48人,从甲地到乙地的营运成本依次为1500元/辆和2000元/辆.公司拟组建一个不超过21辆车的车队,并要求![]() 种型号的车不多于
种型号的车不多于![]() 种型号的车5辆.若每天从甲地运送到乙地的旅客不少于800人,为使公司从甲地到乙地的营运成本最小,应配备
种型号的车5辆.若每天从甲地运送到乙地的旅客不少于800人,为使公司从甲地到乙地的营运成本最小,应配备![]() 、
、![]() 两种型号的车各多少辆?并求出最小营运成本.
两种型号的车各多少辆?并求出最小营运成本.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论:
![]() “直线l与平面
“直线l与平面![]() 平行”是“直线l在平面
平行”是“直线l在平面![]() 外”的充分不必要条件;
外”的充分不必要条件;
![]() 若p:
若p:![]() ,
,![]() ,则
,则![]() :
:![]() ,
,![]() ;
;
![]() 命题“设a,
命题“设a,![]() ,若
,若![]() ,则
,则![]() 或
或![]() ”为真命题;
”为真命题;
![]() “
“![]() ”是“函数
”是“函数![]() 在
在![]() 上单调递增”的充要条件.
上单调递增”的充要条件.
其中所有正确结论的序号为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com